题目内容

数列{a_n}中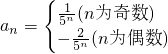， $数学公式$ ，S_2n=a₁+a₂+…+a_2n，则 $数学公式$ =________．

$\text{[math]}$
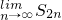分析：根据通项公式的特点，奇数项和偶数项构成等比数列，分别求出奇数项和与偶数项和，然后加在一起求s_2n，再求极限．
解答：∵ $\text{[math]}$
∴当数列的项数为2n时，奇数项和偶数都是n项，
∴奇数项和s₁=a₁+a₃+a₅+…+a_2n-1= $\text{[math]}$
= $\text{[math]}$ = $\text{[math]}$
偶数项和s₂=a₂+a₄+…+a_2n=-2（ $\text{[math]}$ ）
=-2× $\text{[math]}$ =- $\text{[math]}$ （1- $\text{[math]}$ ）
∴s_2n=s₁+s₂= $\text{[math]}$ （1- $\text{[math]}$ ），则 $\text{[math]}$ s_2n= $\text{[math]}$
故答案为： $\text{[math]}$
点评：由通项公式的特点将该数列分成两个等比数列，然后分别求和，也成为分组求和法，即把非特殊数列的求和问题化为等差（等比）数列的求和问题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知数列{a_n}是以d为公差的等差数列，{b_n}数列是以q为公比的等比数列．
（Ⅰ）若数列的前n项和为S_n，且a₁=b₁=d=2，S₃＜a₁₀₀₃+5b₂-2010，求整数q的值；
（Ⅱ）在（Ⅰ）的条件下，试问数列中是否存在一项b_k，使得b_k恰好可以表示为该数列中连续p（p∈N，p≥2）项的和？请说明理由；
（Ⅲ）若b₁=a_r，b₂=a_s≠a_r，b₃=a_t（其中t＞s＞r，且（s-r）是（t-r）的约数），求证：数列{b_n}中每一项都是数列{a_n}中的项．

（1）若对于任意的n∈N^*，总有

成立，求常数A，B的值；
（2）在数列{a_n}中，a1=

（n≥2，n∈N^*），求通项a_n；
（3）在（2）题的条件下，设bn=

，从数列{b_n}中依次取出第k₁项，第k₂项，…第k_n项，按原来的顺序组成新的数列{c_n}，其中cn=bkn，其中k₁=m，k_n+1-k_n=r∈N^*．试问是否存在正整数m，r使

(c1+c2+…+cn)=S且

成立？若存在，求正整数m，r的值；不存在，说明理由．

2、若数列A_n：a₁，a₂，…，a_n（n≥2）满足|a_k+1-a_k|=1（k=1，2，…，n-1），则称A_n为E数列，记S（A_n）=a₁+a₂+…+a_n．
（Ⅰ）写出一个E数列A₅满足a₁=a₃=0；
（Ⅱ）若a₁=12，n=2000，证明：E数列A_n是递增数列的充要条件是a_n=2011；
（Ⅲ）在a₁=4的E数列A_n中，求使得S（A_n）=0成立得n的最小值．

已知数列{a_n}，首项a ₁=3且2a _n=S _n•S _n-1 （n≥2）．
（1）求证：{

}是等差数列，并求公差；
（2）求{a _n }的通项公式；
（3）数列{a_n}中是否存在自然数k₀，使得当自然数k≥k₀时使不等式a_k＞a_k+1对任意大于等于k的自然数都成立，若存在求出最小的k值，否则请说明理由．

在数列{a_n}中，又s，则数列{b_n}的前n项和为________