题目内容
17.求证:(1)函数f(x)=-2x2+3在区间(-∞,0]上是单调增函数;
(2)函数f(x)=-x3+1在区间(-∞,0]上是单调减函数;
(3)函数f(x)=2-$\frac{3}{x}$在区间(-∞,0)和(0,+∞)上都是单调增函数.
分析 (1)在要求证的区间内任取两个自变量x1,x2,规定大小后把对应的函数值作差,因式分解后判断差式的符号,从而得到对应函数值的大小,然后利用增函数的概念得到证明;
(2)(3)根据函数的单调性的定义证明即可.
解答 证明:(1)设x1,x2∈(-∞,0],且x1<x2,
则f(x1)-f(x2)=-2${{x}_{1}}^{2}$+2${{x}_{2}}^{2}$=2(x2+x1)(x2-x1).
∵x1,x2∈[0,+∞),且x1<x2,
∴x1+x2<0,x2-x1>0.
∴2(x2+x1)(x2-x1)<0.
即f(x1)-f(x2)<0.
f(x1)<f(x2).
所以f(x)在区间(-∞,0])上是增函数.
(2))设x1,x2∈(-∞,0],且x1<x2,
则f(x1)-f(x2)=-${{x}_{1}}^{3}$+${{x}_{2}}^{3}$=(x2-x1)(${{x}_{2}}^{2}$+x1x2+${{x}_{1}}^{2}$),
∵x1<x2≤0,∴x2-x1>0,${{x}_{2}}^{2}$+x1x2+${{x}_{1}}^{2}$>0,
∴f(x1)-f(x2)>0,
∴函数f(x)=-x3+1在区间(-∞,0]上是单调减函数;
(3)设x1<x2<0,则:
f(x1)-f(x2)=-$\frac{3}{{x}_{1}}$+$\frac{3}{{x}_{2}}$=$\frac{3{(x}_{1}{-x}_{2})}{{{x}_{1}x}_{2}}$;
∵x1<x2<0;
∴x1-x2<0,x1x2>0;
∴f(x1)<f(x2);
∴f(x)在区间(-∞,0)上是单调增函数,
同理可证函数f(x)=2-$\frac{3}{x}$在区间(0,+∞)上都是单调增函数.
点评 本题考查了函数单调性的判断与证明,训练了因式分解法,解答此题的关键是因式分解要彻底,避免出现证题用题的现象的发生.是基础题.

 阅读快车系列答案
阅读快车系列答案| A. | ?x>0,x2+2x+3>0 | B. | ?x>0,x2+2x+3≥0 | C. | ?x≤0,x2+2x+3<0 | D. | ?x≤0,x2+2x+3≤0 |
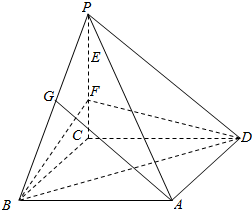 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?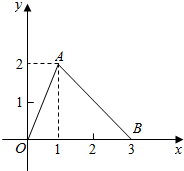 函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).
函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).