Question

7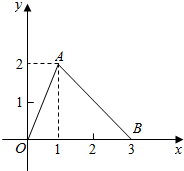．函数f（x）的图象是如图所示的折线段OAB，点A的坐标为（1，2），点B的坐标为（3，0），定义函数g（x）=f（x）（1-x）．
（1）求函数f（x）的解析式．
（2）画出函数g（x）的图象．
（3）求函数g（x）的值域．

Answer 1

分析 本题考查的是分段函数问题．在解答的过程当中应先根据函数f（x）的图象求出解析式，再根据g（x）=f（x）•（x-1）．求的函数g（x）的解析式，结合函数g（x）的解析式即可求的函数g（x）最大值．

解答 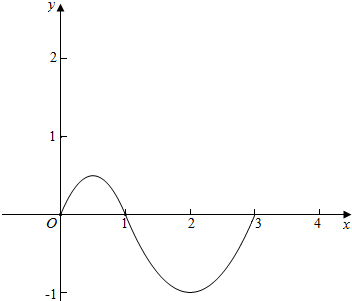解：（1）由题意知：函数f（x）的解析式为：$f（x）=\left\{\begin{array}{l}{2x，0≤x≤1}\\{-x+3，1＜x≤3}\end{array}\right.$，
又∵g（x）=f（x）•（1-x）．
∴函数g（x）的解析式为：$g（x）=\left\{\begin{array}{l}{-2{x}^{2}+2x，0≤x≤1}\\{{x}^{2}-4x+3，1＜x≤3}\end{array}\right.$
（2）函数g（x）的图象如图
（3）当0≤x≤1时，g（x）=-2（x-$\frac{1}{2}$）2+$\frac{1}{2}$，∴g_max（x）=g（$\frac{1}{2}$）=$\frac{1}{2}$，g（x）_min=g（0）=g（1）=0；
当1＜x≤3时，g（x）=（x-2）²-1，g（x）_min=g（2）=-1，g（x）_max=g（3）=0．
∴函数g（x）值域为[-1，$\frac{1}{2}$]．

点评 本题考查的是分段函数解析式的求法和分段函数求最值的综合问题．在解答时充分体现了数形结合的思想、分类讨论的思想以及问题转化的思想．