题目内容
已知函数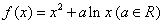 ,求
,求 的单调区间
的单调区间
【解析】函数 的定义域为
的定义域为 .
.
∵ ,∴
,∴ .
.
由于 ,所以
,所以
(1)当 时,
时, ,
, 在
在 上是增函数;
上是增函数;
(2)当 时,
时, .
.
令 ,得
,得 (因
(因 舍去)
舍去)
令 ,解得
,解得 ;令
;令 ,解得
,解得 .
.
此时, 在
在 上是增函数,在
上是增函数,在 上是减函数
上是减函数
综上所述:当 时
时 的单调递增区间是
的单调递增区间是 ;当
;当 时,
时, 的单调递增区间是
的单调递增区间是 ;单调递减区间是
;单调递减区间是 .
.
(2)∵ ,∴
,∴ ,
,
∵函数 在
在 上是减函数,∴
上是减函数,∴ 在
在 上恒成立,
上恒成立,
∴ 在
在 上恒成立,设
上恒成立,设 ,
,
 在
在 上为减函数,∴
上为减函数,∴ ,∴
,∴
∴ 的取值范围是
的取值范围是 .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,则
,则 的最 值为
的最 值为  为曲线
为曲线 :
: 在点
在点 处的切线.
处的切线. 在点
在点 处的切线方程为________.
处的切线方程为________. ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;(2)曲线
的解析式;(2)曲线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值. 在某个区间
在某个区间 内可导
内可导 ,则
,则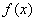 为____函数;若
为____函数;若 ,则
,则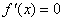 恒成立,则
恒成立,则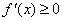 且
且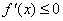 且
且
 .
. 时,求函数
时,求函数 时,求函数
时,求函数 满足
满足 ,
, ,求
,求 .
. 中,若
中,若 ,
, ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.