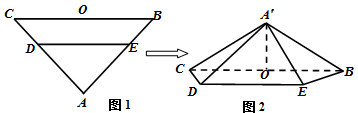
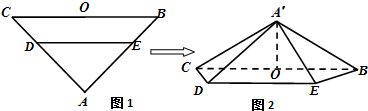
题目内容
在等腰△ABC中,AD为底边BC上的高.在AD上取一点E,使AE=
答案:
解析:
解析:
| 如图所示,
∴AE⊥MN, ∴A′E⊥MN. 又MN∥BC, ∴A′E⊥BC. ∵DE⊥BC, ∴二面角A′—MN—D的平面角为∠A′ED,即∠A′ED=60º. 在△A′DE中,设A′E=a,则DE=2a.又∠A′ED=60º,由余弦定理,得A′D= ∴A′E2+A′D2+DE2,即∠DA′F=90º. ∴A′E⊥A′D.∴A′E⊥平面A′BC. 又A′E |

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

 如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,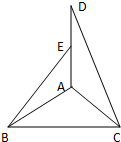 如图,在等腰△ABC中,
如图,在等腰△ABC中,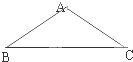 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量