题目内容
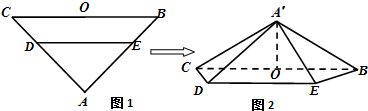 如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=| 2 |
| 3 |
(1)证明:A′O⊥平面BCDE;
(2)求A′D与平面A′BC所成角的正弦值.
分析:(1)利用线面垂直的判定定理证明A′O⊥平面BCDE.
(2)根据线面角的定义,先求出直线和平面所成的角,然后利用三角边长关系求正弦值.
(2)根据线面角的定义,先求出直线和平面所成的角,然后利用三角边长关系求正弦值.
解答: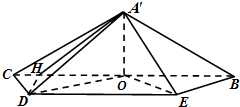 解:(1)在图1中,易得OC=3,AC=3
解:(1)在图1中,易得OC=3,AC=3
,AD=2
连结OD,OE,在△OCD中,
由余弦定理可得OD=
=
由翻折不变性可知A′D=2
,
∴A'O2+OD2=A'D2,
∴A'O⊥OD.
同理可证A'O⊥OE,
又OD∩OE=O,
∴A'O⊥平面BCDE.
(2)过D作DH⊥BC交OC的延长线于H,连结A'H,
∵A'O⊥平面BCDE,A'O?面A'BC,
∴面A'BC⊥面BCDE,
∴DH⊥面A'BC,
∴∠DA'H即为A'D与平面A'BC所成角.
又DH=1,A′D=
=2
,
∴sin∠DA′H=
=
A'D与平面A'BC所成角的正弦值为
.
 解:(1)在图1中,易得OC=3,AC=3
解:(1)在图1中,易得OC=3,AC=3| 2 |
| 2 |
连结OD,OE,在△OCD中,
由余弦定理可得OD=
| OC2+CD2-2OC•CDcos45° |
| 5 |
由翻折不变性可知A′D=2
| 2 |
∴A'O2+OD2=A'D2,
∴A'O⊥OD.
同理可证A'O⊥OE,
又OD∩OE=O,
∴A'O⊥平面BCDE.
(2)过D作DH⊥BC交OC的延长线于H,连结A'H,
∵A'O⊥平面BCDE,A'O?面A'BC,
∴面A'BC⊥面BCDE,
∴DH⊥面A'BC,
∴∠DA'H即为A'D与平面A'BC所成角.
又DH=1,A′D=
| OD2+A′O2 |
| 2 |
∴sin∠DA′H=
| DH |
| A′D |
| ||
| 4 |
| ||
| 4 |
点评:本题主要考查直线和平面垂直的判定定理以及直线和平面所成角的大小,要求熟练掌握相应的判定定理和线面所成角的求法.

练习册系列答案
相关题目

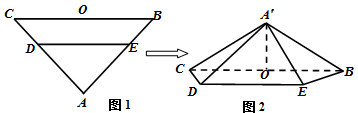

 ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′-BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′-BCDE,其中A′O= .
.