题目内容
已知向量
、
满足|
|=|
|=1，且
•
=0，则cos＜2
+
，
＞= ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的夹角公式，求出（2
+
）•
，|2
+
|，代入公式即可得到所求值．
| a |
| b |
| b |
| a |
| b |
解答：
解：由于向量
、
满足|
|=|
|=1，且
•
=0，
则（2
+
）•
=2
•
+
2=1，
|2
+
|=
=
=
，
则cos＜2
+
，
＞=
=
=
．
故答案为：
．
| a |
| b |
| a |
| b |
| a |
| b |
则（2
| a |
| b |
| b |
| a |
| b |
| b |
|2
| a |
| b |
(2
|
4
|
| 5 |
则cos＜2
| a |
| b |
| b |
(2
| ||||||
|2
|
| 1 | ||
|
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查平面向量的数量积的定义和夹角公式，考查运算能力，属于基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
表面积为4
的正四面体的各个顶点都在同一个球面上，则此球的体积为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各组函数f（x）与g（x）的图象相同的是（ ）
A、f（x）=x，g（x）=（
| |||||
| B、f（x）=x2，g（x）=（x+1）2 | |||||
C、f（x）=|x|，g（c）=
| |||||
| D、f（x）=1，g（x）=x0 |
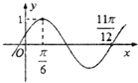函数f（x）=Asin（ωx+∅）（A＞0，ω＞0，|∅|＜| π |
| 2 |
| 1 |
| 2 |
A、y=sin（4x+
| ||
B、y=sin（4x+
| ||
C、y=sin（x+
| ||
D、y=sin（x+
|
某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为（ ）
A、
| ||
B、
| ||
C、2
| ||
| D、3 |