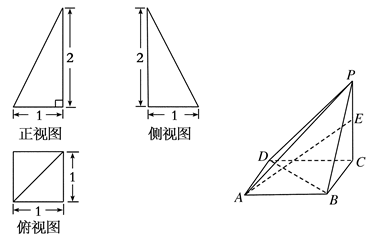
题目内容
四棱锥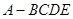 的侧面
的侧面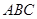 是等边三角形,
是等边三角形,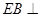 平面
平面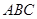 ,
,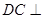 平面
平面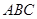 ,
,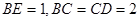 ,
,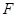 是棱
是棱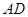 的中点.
的中点.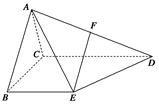
(1)求证: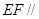 平面
平面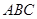 ;
;
(2)求四棱锥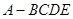 的体积.
的体积.
(1)见解析(2) 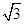
解析试题分析:(1)取AC中点M,连结FM、BM,
∵F是AD中点,∴FM∥DC,且FM=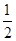 DC=1,
DC=1,
∵EB⊥平面ABC,DC⊥平面ABC,∴EB∥DC,∴FM∥EB.
又∵EB=1,∴FM=EB,
∴四边形BEFM是平行四边形,∴EF∥BM,
∵EF?平面ABC,BM?平面ABC,∴EF∥平面ABC.
(2)取BC中点N,连结AN,∵AB=AC,∴AN=BC,∵EB⊥平面ABC,∴AN⊥EB,
∵BC与EB是底面BCDE内的相交直线,∴AN⊥平面BCDE,
由(1)得,底面BCDE为直角梯形,S梯形BCDE=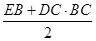 =3,
=3,
在等边△ABC中,BC=2,∴AN=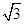 ,∴V棱锥A-BCDE=
,∴V棱锥A-BCDE=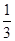 S梯形BCDE·AN=
S梯形BCDE·AN=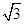 .
.
考点:空间线面平行的判定定理及锥体体积公式
点评:题目较简单,学生易得分

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
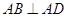 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.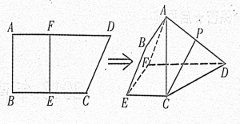
 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.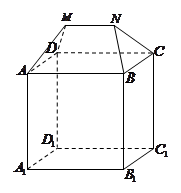

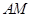 与平面
与平面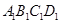 所成角的正弦值;
所成角的正弦值;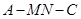 的余弦值;
的余弦值; 底面
底面 为菱形,
为菱形, 平面
平面 ,
,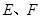 分别是
分别是 、
、 的中点.
的中点. 
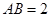 , 若
, 若 为线段
为线段 上的动点,
上的动点,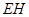 与平面
与平面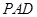 所成的最大角的正切值为
所成的最大角的正切值为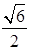 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.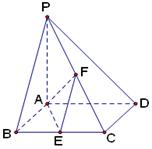
 中,底面
中,底面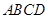 是直角梯形,
是直角梯形,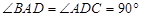 ,
, ,
,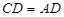 .
.
 是二面角
是二面角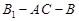 的平面角;
的平面角; 上是否存一点
上是否存一点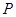 ,使得
,使得 与平面
与平面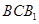 与平面
与平面 都平行?证明你的结论.
都平行?证明你的结论.
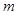 ),则该几何体的体积。
),则该几何体的体积。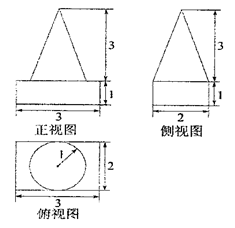
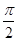 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1. 