题目内容
(本小题满分1 2分)
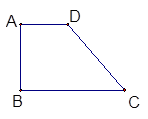
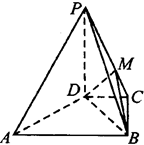
如图,四边形ABCD中,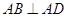 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.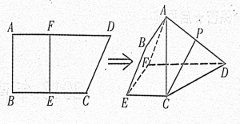
( I )当E为BC中点时,求证:CP//平面ABEF
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值。
(1)根据线面平行的判定定理来证明。
(2)当 时,
时, 有最大值,最大值为3.
有最大值,最大值为3.
解析试题分析:解:(Ⅰ)取 的中点
的中点 ,连
,连 、
、 ,
,
则

 ,又
,又 ∥
∥ ,
,
所以

 ,即四边形
,即四边形 为平行四边形,
为平行四边形,
所以 ∥
∥ ,又
,又 平面
平面 ,
, ,
,
故 ∥平面
∥平面 .
.
(Ⅱ)因为平面 平面
平面 ,平面
,平面 平面
平面 ,
,
又
所以 平面
平面
由已知 ,所以
,所以
故



所以,当 时,
时, 有最大值,最大值为3.
有最大值,最大值为3.
考点:本试题考查了线面平行的判定定理,以及几何体体积的运用,。
点评:解决该试题的关键是利用已知的线线平行证明线面平行,同时设出变量,结合体积的公式得到关于x的函数关系式,进而利用函数的性质来求解最值,注意熟练的结合二次函数的对称轴和定义域来求解最值,属于中档题。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
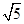 .
.
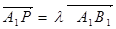
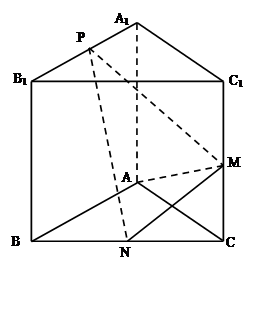
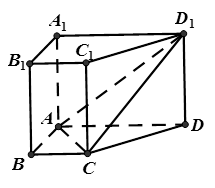
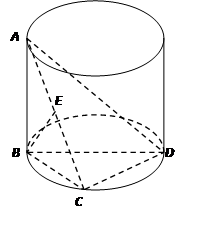
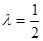 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.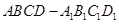 中,
中,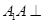 面
面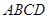 ,底面
,底面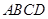 是直角梯形,
是直角梯形,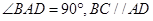 ,
,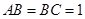 ,
,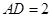 ,异面直线
,异面直线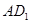 与
与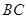 所成角为
所成角为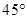 .
.
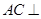 平面
平面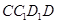 ;
;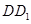 与平面
与平面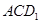 所成角的正弦值.
所成角的正弦值.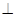 平面PEG.
平面PEG.
 .
.
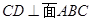 ;
;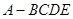 的侧面
的侧面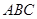 是等边三角形,
是等边三角形,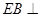 平面
平面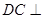 平面
平面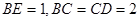 ,
,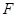 是棱
是棱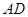 的中点.
的中点.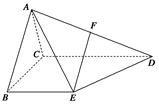
 平面
平面