题目内容
设数列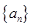 前
前 项和为
项和为 ,点
,点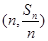
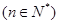 均在函数
均在函数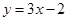 图象上。
图象上。
(1)求数列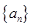 的通项公式;
的通项公式;
(2)设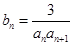 ,
,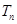 是数列
是数列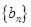 的前
的前 项和,求使得
项和,求使得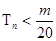 对所有
对所有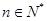 都成立的最小正整数
都成立的最小正整数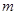 。
。
【答案】
(1) an=6n-5 ( )
)
(2) 10.
【解析】解:(1)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)= 2ax+b,由于f`(x)=6x-2,得a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数 的图像上,所以
的图像上,所以 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)- =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 ( )
)
(2)由(1)得知 =
= =
= ,
,
故Tn= =
=
 =
= (1-
(1- ).
).
因此,要使 (1-
(1- )<
)< (
( )成立的m,必须且仅须满足
)成立的m,必须且仅须满足 ≤
≤ ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 前
前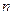 项和为
项和为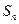 ,点
,点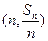
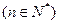 均在函数
均在函数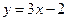 图象上。
图象上。 项公式;
项公式;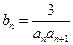 ,
,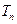 是数列
是数列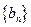 的前
的前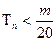 对所有
对所有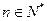 都成立的最小正整数
都成立的最小正整数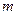 。
。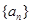 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图像上.
的图像上. ,
, 是数列
是数列 的前
的前 对所有
对所有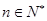 都成立的最小正整数
都成立的最小正整数 .
.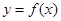 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为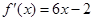 ,数列
,数列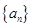 的前
的前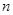 项和为
项和为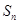 ,点
,点
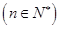 均在函数
均在函数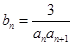 ,
, 是数列
是数列 的前
的前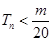 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。