题目内容
20.已知函数f(x)=x2-2x+3,当0≤x≤m时,该函数有最大值3,最小值2,则实数m的取值范围是( )| A. | [1,+∞) | B. | [0,2] | C. | (-∞,2] | D. | [1,2] |
分析 对f(x)配方得到f(x)=(x-1)2+2,从而便可看出f(0)=3,f(1)=2,f(2)=3,从而根据f(x)在[0,m]上有最大值3,最小值2,便可得到1≤m≤2,这便得出了实数m的取值范围.
解答 解:f(x)=(x-1)2+2;
x=0时,f(x)=3,x=1时,f(x)=2,x=2时,f(x)=3;
∵当0≤x≤m时,该函数有最大值3,最小值2;
∴1≤m≤2;
即实数m的取值范围为[1,2].
故选:D.
点评 配方法求二次函数在闭区间上的最大值、最小值,要熟悉二次函数的图象,并且可结合二次函数f(x)的图象.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,以下说法正确的是( )
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
9.已知$\overrightarrow{AB}$=(-1,-2),$\overrightarrow{BC}$=(-3,-4),则$\overrightarrow{CA}$=( )
| A. | (4,6) | B. | (-4,-6) | C. | (2,2) | D. | (-2,-2) |
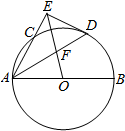 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.