题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,以下说法正确的是( )| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
分析 运用单调性的定义,即可判断A错;取m=1,可判断B;求得各段的值域,即可判断C;取m=1,即可判断D.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,
当x<0时,函数y=ex递增,当x≥0时,y=x+m递增,
但当e0>m,即m<1,函数f(x)在R上不单调,故A错;
当m=1时,f(x)=0无解,故B错;
当x<0时,函数f(x)∈(0,1),当x≥0时,f(x)≥m,
则f(x)取不到最大值,故C错;
当m=1时,当x<0时,函数f(x)∈(0,1),当x≥0时,f(x)≥1,
f(x)的值域为(0,+∞),取不到最小值,故D对.
故选:D.
点评 本题考查分段函数的运用:求单调性和最值,考查特殊值法的运用,属于中档题和易错题.

练习册系列答案
相关题目
5.已知A(1,5),B(5,-2),在x轴上存在一点M,使|MA|=|MB|,则点M的坐标为( )
| A. | $(\frac{8}{3},0)$ | B. | $(\frac{3}{8},0)$ | C. | $(-\frac{8}{3},0)$ | D. | $(-\frac{3}{8},0)$ |
20.已知函数f(x)=x2-2x+3,当0≤x≤m时,该函数有最大值3,最小值2,则实数m的取值范围是( )
| A. | [1,+∞) | B. | [0,2] | C. | (-∞,2] | D. | [1,2] |
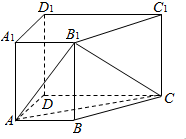 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).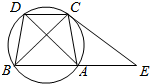 如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.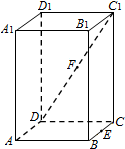 在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: