题目内容
5.已知f(x)是定义在R上的不恒为零的函数,且对任意的a,b∈R都满足:f(a•b)=af(b)+bf(a),若f(2)=2,Un=f(2n)(n∈N*)(1)求Ul,U2,U3的值.
(2)求证:Un+1>Un.
分析 (1)由题意可令a=2,b=2n-1(n∈N*),然后分别取n为1,2,3求得Ul,U2,U3的值.
(2)由(1)猜测f(2n)=n×2n(n∈N*),然后利用数学归纳法证得结论,再由${U}_{n+1}-{U}_{n}>0(n∈{N}^{*})$证得Un+1>Un.
解答 (1)解:令a=2,b=2n-1(n∈N*),
当n=1时,${U}_{1}=f(2)=2=1×{2}^{1}$,
当n=2时,${U}_{2}=f(2×2)=f({2}^{2})=2f(2)+2f(2)=2×{2}^{2}$,
当n=3时,${U}_{3}=f(2×{2}^{2})=2f({2}^{2})+{2}^{2}f(2)=3×{2}^{3}$,
∴U1=2,U2=8,U3=24;
(2)由(1)猜测f(2n)=n×2n(n∈N*).
用数学归纳法证明如下:
①当n=1时,f(2)=1×2,结论成立;
②假设n=k时结论成立,即f(2k)=k×2k,
当n=k+1时,f(2k+1)=f(2×2k)=2f(2k)+2kf(2)=2×k×2k+2k×2=k×2k+1+2k+1=(k+1)×2k+1.
∴n=k+1时,结论成立.
由①②可知,对n∈N*,
f(2n)=n×2n.
∴${U}_{n}=f({2}^{n})=n×{2}^{n}(n∈{N}^{*})$.
要证明Un+1>Un,只需证明${U}_{n+1}-{U}_{n}>0(n∈{N}^{*})$,
∵${U}_{n+1}-{U}_{n}=(n+1)•{2}^{n+1}-n•{2}^{n}={2}^{n}(n+2)>0$,
∴Un+1>Un.
点评 本题考查数列的函数特性,考查了利用数学归纳法证明与自然数有关的命题,正确理解题意,合理设出a,b的值是解答该题的关键,属中高档题.

 阅读快车系列答案
阅读快车系列答案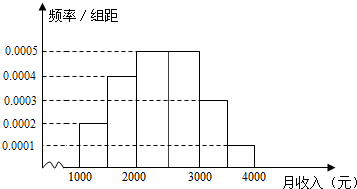 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )| A. | 2360 | B. | 2380 | C. | 2400 | D. | 2420 |
| A. | [1,+∞) | B. | [0,2] | C. | (-∞,2] | D. | [1,2] |
| A. | (x+2)2=3 | B. | (x-2)2=3 | C. | (x-2)2=5 | D. | (x+2)2=5 |
