题目内容
8.已知f(α)=$\frac{sin(π-α)cos(2π-α)tan(-α+\frac{3π}{2})}{cos(-π-α)}$,(1)求f(-$\frac{31π}{3}$)的值;
(2)若2f(π+α)=f($\frac{π}{2}$+α),求$\frac{sinα+cosα}{sinα-cosα}$+cos2α的值;
(3)若f(α)=$\frac{3}{5}$,求sinα,tanα的值.
分析 (1)利用诱导公式可得f(α)=-cosα,从而可求f(-$\frac{31π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$.
(2)由题意-2cos(π+α)=-cos($\frac{π}{2}$+α),解得2cosα=sinα,tanα=2,由同角三角函数基本关系的运用即可求职.
(3)由f(α)=$\frac{3}{5}$,可求cosα=-$\frac{3}{5}$,利用同角三角函数基本关系的运用即可得解.
解答 解:(1)∵f(α)=$\frac{sin(π-α)cos(2π-α)tan(-α+\frac{3π}{2})}{cos(-π-α)}$=$\frac{sinαcosαcotα}{-cosα}$=-cosα,
∴f(-$\frac{31π}{3}$)=-cos(-$\frac{31π}{3}$)=-cos(10$π+\frac{π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$.
(2)∵2f(π+α)=f($\frac{π}{2}$+α),
∴-2cos(π+α)=-cos($\frac{π}{2}$+α),解得2cosα=sinα,tanα=2,
∴$\frac{sinα+cosα}{sinα-cosα}$+cos2α=3+$\frac{1+cos2α}{2}$=3+$\frac{1+\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}}{2}$=3+$\frac{1}{5}$=$\frac{16}{5}$.
(3)∵f(α)=$\frac{3}{5}$,求sinα,tanα
∴-cosα=$\frac{3}{5}$,即cosα=-$\frac{3}{5}$,
∴sin$α=±\sqrt{1-co{s}^{2}α}$=$±\frac{4}{5}$,tan$α=\frac{sinα}{cosα}$=$±\frac{4}{3}$.
点评 本题主要考查了运用诱导公式化简求值,同角三角函数基本关系的运用,熟练掌握诱导公式是解题的关键,属于基础题.

 步步高达标卷系列答案
步步高达标卷系列答案| A. | 2012 | B. | 4024 | C. | 2014 | D. | 4025 |
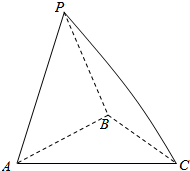 如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.
如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.