题目内容
已知函数 。
。
(1)当a=3时,求不等式 的解集;
的解集;
(2)若 对
对 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
(1) 或
或 ;(2)
;(2) .
.
解析试题分析:(1)利用零点分段法去绝对值,分为三种情况,当 时,当
时,当 ,当
,当 时解不等式;求三个交集,一个并集,最终结果写成集合形式;
时解不等式;求三个交集,一个并集,最终结果写成集合形式;
(2)将原不等式转化为 恒成立,画图
恒成立,画图 ,
, 的图像,满足恒成立的图像,要求
的图像,满足恒成立的图像,要求 始终在
始终在 的上面,而
的上面,而 的图像时折线,折点坐标为
的图像时折线,折点坐标为 ,让
,让 与端点值比较大小,同时得到
与端点值比较大小,同时得到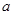 的取值范围.
的取值范围.
试题解析:(1) 时,即求解
时,即求解
①当 时,
时,
②当 时,
时,
③当 时,
时,
综上,解集为 5分
5分
(2)即 恒成立
恒成立
令 则函数图象为
则函数图象为 ,
, ..10分
..10分
考点:1.解绝对值不等式;2.利用函数图象解不等式.

练习册系列答案
相关题目
 在点
在点 处的切线方程为
处的切线方程为
 .
. 、
、 的值;
的值;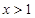 时,
时, 恒成立,求实数
恒成立,求实数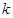 的取值范围;
的取值范围; ,且
,且 时,
时, .
.
 .
. 的单调区间和极值;
的单调区间和极值; 对
对 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明.
的单调性,并用定义证明. ,不等式
,不等式  恒成立,求
恒成立,求 的取值范围;
的取值范围; 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有 ,且当
,且当 时,
时, 。
。 是否满足这些条件;
是否满足这些条件; ,求方程
,求方程 的解。
的解。 ,试求函数的零点个数.
,试求函数的零点个数. -
- +1的最小值与最大值.
+1的最小值与最大值. 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
. ;
; ,求区间
,求区间 .
.