题目内容
不等式：2|x-2|+|x-4|＞26的解集为________．
{x|x＜0或x＞6}
分析：由题意可得|x-2|+|x-4|＞6，对x分类讨论，去掉绝对值符号即可求得答案．
解答：∵2|x-2|+|x-4|＞26，y=2x为增函数，
∴|x-2|+|x-4|＞6，令g（x）=|x-2|+|x-4|，
若x≤2，g（x）=6-2x，由6-2x＞6得x＜0，
∴x＜0；
若2＜x＜4，g（x）=x-2+4-x=2，不符合题意，x∈∅；
若x≥4，g（x）=2x-6＞6，解得x＞6，
综上所述，x＜0或x＞6．
故答案为：{x|x＜0或x＞6}．
点评：本题考查指数型复合函数的性质及应用，对x分类讨论，去掉绝对值符号是关键，属于中档题．
分析：由题意可得|x-2|+|x-4|＞6，对x分类讨论，去掉绝对值符号即可求得答案．
解答：∵2|x-2|+|x-4|＞26，y=2x为增函数，
∴|x-2|+|x-4|＞6，令g（x）=|x-2|+|x-4|，
若x≤2，g（x）=6-2x，由6-2x＞6得x＜0，
∴x＜0；
若2＜x＜4，g（x）=x-2+4-x=2，不符合题意，x∈∅；
若x≥4，g（x）=2x-6＞6，解得x＞6，
综上所述，x＜0或x＞6．
故答案为：{x|x＜0或x＞6}．
点评：本题考查指数型复合函数的性质及应用，对x分类讨论，去掉绝对值符号是关键，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
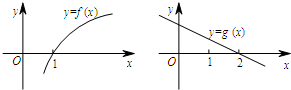函数y=f（x），y=g（x）的图象如下，f（1）=g（2）=0，不等式| f(x) |
| g(x) |
| A、{x|x＜1或x＞2}∪{x|1＜x＜2} |
| B、{x|1≤x＜2} |
| C、{x|x≤1或x＞2}∪{x|1＜x＜2} |
| D、{x|1≤x≤2} |