题目内容
已知函数 ,
,
(1) 当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)求函数 的单调区间.
的单调区间.
(1)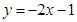
(2)①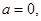
 的单调递减区间为
的单调递减区间为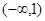 ,
,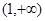 ,
,
②当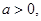
 的单调递减区间为
的单调递减区间为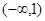 ,
,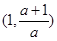 ,单调递增区间为
,单调递增区间为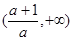 ,
,
③当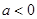 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为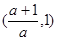
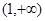 .
.
解析试题分析:(1)解:当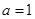 时,
时, ,
,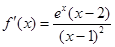 ,
,
所以 在
在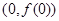 处的切线方程为
处的切线方程为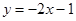 ,
,
(II)解: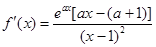 ,当
,当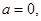 时
时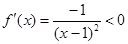 ,
,
又函数的定义域为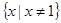 , 所以
, 所以 的单调递减区间为
的单调递减区间为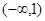 ,
,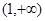 ,
,
当 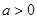 时,
时, 的单调递减区间为
的单调递减区间为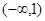 ,
,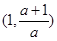 ,单调递增区间为
,单调递增区间为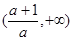 ,
,
当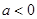 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为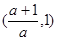
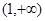 .
.
考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.
点评:本题以三次函数为载体,主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (
( )是定义在
)是定义在 上的奇函数,且
上的奇函数,且 时,函数
时,函数 取极值1.
取极值1. ,若
,若 (
( ),不等式
),不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; (
( )的图象如图.根据图象写出:
)的图象如图.根据图象写出:
 的
的 值.
值.

 的不等式
的不等式 
 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。 (
( )是偶函数
)是偶函数 的值;
的值; ,若函数
,若函数 与
与 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围
的取值范围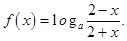 .
. 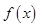 的定义域;
的定义域; 在其定义域上的奇偶性,并予以证明,
在其定义域上的奇偶性,并予以证明, 的解集。
的解集。 .
. ,解不等式
,解不等式 ;
; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,解不等式
,解不等式 .
.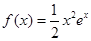 .
.