题目内容
13.若${a_n}=\left\{{\begin{array}{l}{(4-\frac{2}{3}a)n-3,n≤6}\\{{a^{n-5}},n>6}\end{array}}\right.$,a∈N*,且数列{an}是递增数列,则a的值是( )| A. | 4或5 | B. | 3或4 | C. | 3或2 | D. | 1或2 |
分析 由${a_n}=\left\{{\begin{array}{l}{(4-\frac{2}{3}a)n-3,n≤6}\\{{a^{n-5}},n>6}\end{array}}\right.$,a∈N*,且数列{an}是递增数列,可得$(4-\frac{2}{3}a)$×6-3<a2,$4-\frac{2}{3}a$>0,a∈N*,解出即可得出.
解答 解:∵${a_n}=\left\{{\begin{array}{l}{(4-\frac{2}{3}a)n-3,n≤6}\\{{a^{n-5}},n>6}\end{array}}\right.$,a∈N*,且数列{an}是递增数列,
∴$(4-\frac{2}{3}a)$×6-3<a2,$4-\frac{2}{3}a$>0,a∈N*,
解得6>a>3,因此a=4或5.
故选:A.
点评 本题考查了数列的单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.方程x2+y2+2x+4y+6=0表示的图形是( )
| A. | 点 | B. | 两条直线 | C. | 圆 | D. | 没有图形 |
8.已知y=f(x)是奇函数,且f(4)=5,那么f(4)+f(-4)的值为( )
| A. | -5 | B. | 0 | C. | 10 | D. | -10 |
5.“a>0,b>0”是“方程ax2+by2=1表示椭圆”的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 既不充分也不必要条件 |
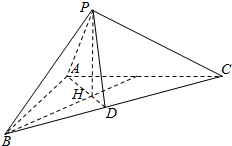 如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.
如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.