题目内容
已知M=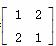 ,β=
,β=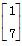 ,计算M5β.
,计算M5β.
解:矩阵M的特征多项式为f(λ)= =λ2-2λ-3.
=λ2-2λ-3.
令f(λ)=0,解得λ1=3,λ2=-1,从而求得对应的一个特征向量分别为α1= ,α2=
,α2= .
.
令β=mα1+nα2,则m=4,n=-3.
M5β=M5(4α1-3α2)
=4(M5α1)-3(M5α2)
=4(λ α1)-3(λ
α1)-3(λ α2)
α2)
=

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
题目内容
已知M=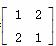 ,β=
,β=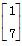 ,计算M5β.
,计算M5β.
解:矩阵M的特征多项式为f(λ)= =λ2-2λ-3.
=λ2-2λ-3.
令f(λ)=0,解得λ1=3,λ2=-1,从而求得对应的一个特征向量分别为α1= ,α2=
,α2= .
.
令β=mα1+nα2,则m=4,n=-3.
M5β=M5(4α1-3α2)
=4(M5α1)-3(M5α2)
=4(λ α1)-3(λ
α1)-3(λ α2)
α2)
=

 一线名师提优试卷系列答案
一线名师提优试卷系列答案