题目内容
2.设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R,求f(x)的单调区间.分析 求出函数的导数,通过讨论a的范围,求出函数的单调区间即可.
解答 解:f(x)=(x-1)3-ax-b,
f′(x)=3(x-1)2-a,
a≤0时,f′(x)>0,f(x)在R递增,
a>0时,令f′(x)>0,解得:x>$\frac{3+\sqrt{3a}}{3}$或x<$\frac{3-\sqrt{3a}}{3}$,
令f′(x)<0,解得:$\frac{3-\sqrt{3a}}{3}$<x<$\frac{3+\sqrt{3a}}{3}$,
故f(x)在(-∞,$\frac{3-\sqrt{3a}}{3}$)递增,在($\frac{3-\sqrt{3a}}{3}$,$\frac{3+\sqrt{3a}}{3}$)递减,在($\frac{3+\sqrt{3a}}{3}$,+∞)递增.
点评 本题考查了导数的应用,考查函数的单调性以及分类讨论思想,是一道基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
11.设a、b分别是甲、乙各抛掷一枚骰子得到的点数,已知乙所得的点数为2,则方程x2+ax+b=0有两个不相等的实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
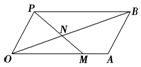 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.