题目内容
 在直三棱柱A1B1C1-ABC中如图1,AC⊥BC,D为AB中点,CB=1,AC=
在直三棱柱A1B1C1-ABC中如图1,AC⊥BC,D为AB中点,CB=1,AC=| 3 |
| 1 |
| 4 |
(1)在图2中画出此三棱柱的左视图和俯视图;
(2)求三棱锥C1-CBD的体积.
考点:由三视图求面积、体积
专题:计算题,作图题
分析:作三视图要求,长对正,高平齐,宽相等;由平行作出异面直线A1B1与C1D所成角,通过解三角形解出边长,求体积.
解答:
解:(1) 左视图为边长为
左视图为边长为
的正方形,
俯视图为直角边1,
的直角三角形.
(2)∵AB∥A1B1,
∴∠C1DB为异面直线A1B1与C1D所成角,
D为Rt△ABC斜边AB的中点,
∴CD=CB,
由三角形全等可得:
C1D=C1B,由∠C1DB=arccos
可得:C1D=C1B=2,
∴AA1=
=
,
∴VC1-CBD=
•
•
•
=
.
 左视图为边长为
左视图为边长为| 3 |
俯视图为直角边1,
| 3 |
(2)∵AB∥A1B1,
∴∠C1DB为异面直线A1B1与C1D所成角,
D为Rt△ABC斜边AB的中点,
∴CD=CB,
由三角形全等可得:
C1D=C1B,由∠C1DB=arccos
| 1 |
| 4 |
∴AA1=
| 22-1 |
| 3 |
∴VC1-CBD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 4 |
点评:三视图要保证长对正,高平齐,宽相等;同时考查了异面直线A1B1与C1D所成角的作法及三角形中求解边长.属于基础题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.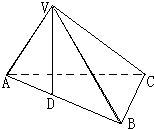 如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.
如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.