题目内容
(本小题满分12分)四棱锥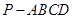 的底面是正方形,
的底面是正方形,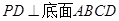 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=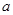 ,
,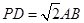
(Ⅰ)求证:平面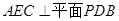 ;
;
(Ⅱ)若E为PB的中点时,求AE与平面PDB所成的角的大小.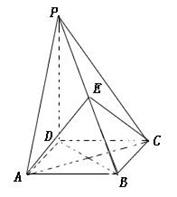
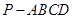 的底面是正方形,
的底面是正方形,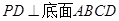 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=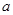 ,
,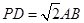
(Ⅰ)求证:平面
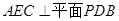 ;
; (Ⅱ)若E为PB的中点时,求AE与平面PDB所成的角的大小.

(Ⅰ)见解析;(Ⅱ)AE与平面PDB所成的角的大小为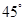 .
.
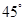 .
. 本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题。
(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;
(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.
解:以D为原点建立空间直角坐标系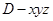 ,
,
设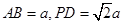 则,
则,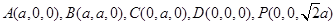
(Ⅰ)∵,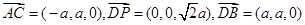 ∴
∴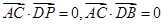 ,
,
∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面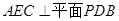 .---------6分
.---------6分
(Ⅱ)当E为PB的中点时,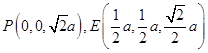 ,
,
设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵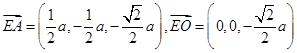 ,
,
∴ ,
,
∴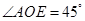 ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为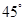 .---------12分
.---------12分
(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;
(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.
解:以D为原点建立空间直角坐标系
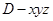 ,
,设
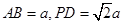 则,
则,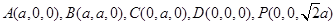
(Ⅰ)∵,
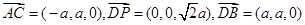 ∴
∴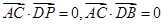 ,
,∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面
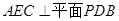 .---------6分
.---------6分(Ⅱ)当E为PB的中点时,
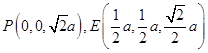 ,
,设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵
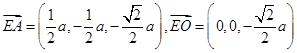 ,
,∴
 ,
,∴
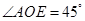 ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为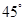 .---------12分
.---------12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
,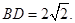

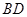 ⊥平面
⊥平面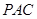 ;
;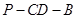 的大小;
的大小; 到平面
到平面 的距离.
的距离.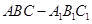 中,侧棱
中,侧棱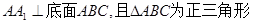 ,点
,点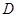 是
是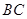 的中点,
的中点,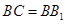 .
.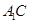 ∥平面
∥平面 ;
;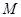 为棱
为棱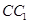 的中点,试证明:
的中点,试证明: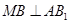 .
.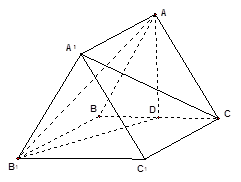
 中,所有的棱长都为2,
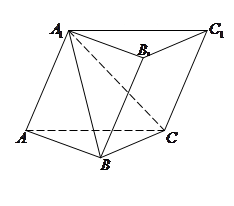
中,所有的棱长都为2,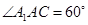 .
.
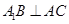 ;
; 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.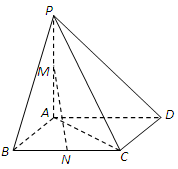
 中,
中,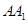 与
与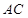 、
、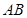 所成角均为
所成角均为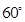 ,
, ,且
,且 ,则三棱锥
,则三棱锥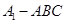 的体积为( )
的体积为( )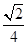
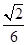
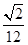
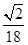
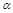 、
、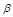 为两个不同的平面,
为两个不同的平面,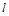 、
、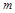 、
、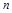 为三条互不相同的直线,
为三条互不相同的直线,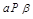 ,
,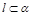 ,则
,则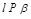 ;
;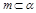 ,
,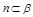 ,
,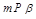 ,
,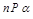 ,则
,则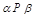 ;
;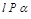 ,
,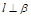 ,则
,则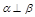 ;
;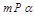 ,
,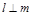 ,
,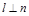 ,则
,则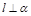 .
.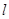 ∥平面
∥平面 ,直线
,直线 ,则
,则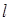 与
与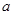 的位置关系是 ( )
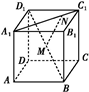
的位置关系是 ( ) A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 .
A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 .