题目内容
(本小题13分)如图,棱锥 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
, ,
,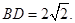

(1)求证: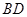 ⊥平面
⊥平面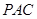 ;
;
(2)求二面角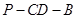 的大小;
的大小;
(3)求点 到平面
到平面 的距离.
的距离.
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
, ,
,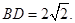

(1)求证:
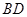 ⊥平面
⊥平面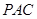 ;
;(2)求二面角
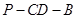 的大小;
的大小;(3)求点
 到平面
到平面 的距离.
的距离.(1)见解析;(2)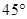 ;(3)
;(3)
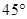 ;(3)
;(3)
试题分析:(方法一)证明:(1)在
 中,
中, ,
,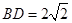 ,
,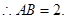
所以
 为正方形,因此
为正方形,因此 . ∵
. ∵ ⊥平面
⊥平面 ,
, 平面
平面 ,
,∴
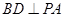 .又∵
.又∵ , ∴
, ∴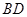 ⊥平面
⊥平面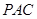 . ……4分
. ……4分 (2)解:由
 ⊥平面
⊥平面 ,知
,知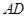 为
为 在平面
在平面 内的射影,
内的射影,又
 ,∴
,∴ ,知
,知 为二面角
为二面角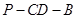 的平面角.
的平面角. 又∵
 ,∴
,∴ . ……9分
. ……9分 (3)∵
 ,∴
,∴ ,
,设
 到面
到面 的距离为
的距离为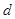 ,
,由
 ,有
,有 ,
, 即
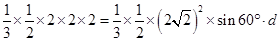 ,
,得
 . ……14分
. ……14分 (方法二)证明:(Ⅰ)建立如图所示的直角坐标系,

则
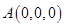 、
、 、
、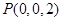 .
.在
 中,
中, ,
,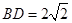 ,
,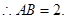 ∴
∴ ,
,∴
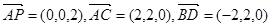 ∵
∵ ,
,即
 ,又∵
,又∵ , ∴
, ∴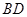 ⊥平面
⊥平面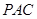 . ……4分
. ……4分 解:(2)由(Ⅰ)得
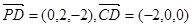 .
. 设平面
 的法向量为
的法向量为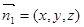 ,则
,则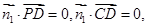
即
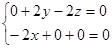 ,∴
,∴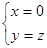 故平面
故平面 的法向量可取为
的法向量可取为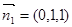
∵
 ⊥平面
⊥平面 ,∴
,∴ 为平面
为平面 的法向量.
的法向量. 设二面角
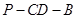 的大小为
的大小为 ,依题意可得
,依题意可得 ,
,∴
 ……9分
……9分 (3)由(Ⅰ)得
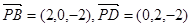 ,
,设平面
 的法向量为
的法向量为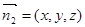 ,
,则
 ,即
,即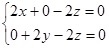 ,∴
,∴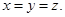 ,
,故平面
 的法向量可取为
的法向量可取为 .
. ∵
 ,∴
,∴ 到面
到面 的距离为
的距离为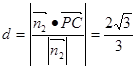 . ……14分
. ……14分点评:解决空间中的平行、垂直以及距离等问题,有传统方法和向量方法两种方法,用传统方法时,要注意紧扣定理,把符合定理的条件都列出来;用向量方法时,运算量较大,要仔细、快速进行.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 ,O为AB的中点.
,O为AB的中点.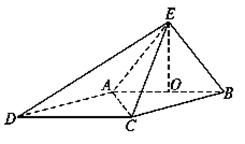
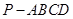 中,底面
中,底面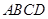 是矩形,
是矩形,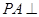 平面
平面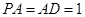 ,
,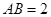 ,
,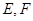 分别是
分别是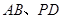 的中点.
的中点.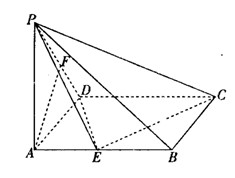
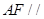 平面
平面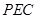 ;
; 的余弦值.
的余弦值. 所在的平面与正方形
所在的平面与正方形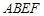 所在的平面相互垂直,
所在的平面相互垂直,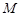 、
、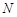 分别是
分别是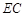 、
、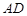 的中点.
的中点.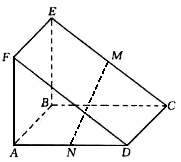
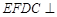 面
面 ;
;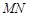 与平面
与平面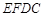 所成的角正弦值.
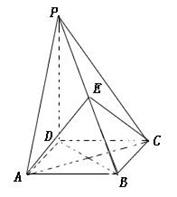
所成的角正弦值.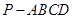 的底面是正方形,
的底面是正方形,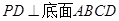 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=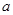 ,
,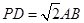
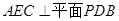 ;
; 
 AD=1,CD=
AD=1,CD=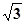 .
.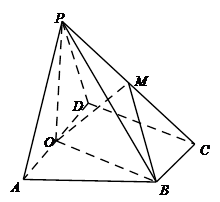
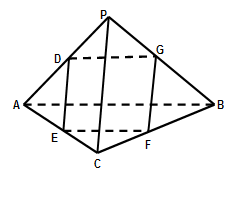
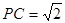 ,求四面体PABC的体积.
,求四面体PABC的体积.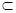 M,b
M,b ,
,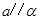 ,
,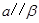 ,则
,则 与
与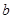 的位置关系是_______.
的位置关系是_______.