题目内容
(本小题满分l2分)已知函数 (
( ).
).
(Ⅰ)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)
 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试求角B和角C.
试求角B和角C.
 (
( ).
).(Ⅰ)求函数
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; (Ⅱ)

 内角
内角 的对边长分别为
的对边长分别为 ,若
,若
 且
且 试求角B和角C.
试求角B和角C.(Ⅰ)函数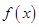 的最小正周期为
的最小正周期为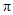 ;递增区间为
;递增区间为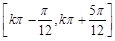 (
(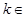 Z );
Z );
(Ⅱ)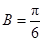 .
. 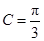
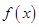 的最小正周期为
的最小正周期为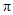 ;递增区间为
;递增区间为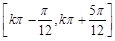 (
(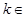 Z );
Z );(Ⅱ)
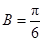 .
. 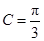
本试题主要是考查了三角函数的性质和解三角形中正弦定理的运用,求解角的综合试题。
(1)因为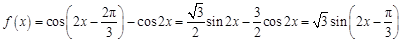 ,然后利用函数的周期公式和单调性得到结论。
,然后利用函数的周期公式和单调性得到结论。
(2)根据上一问得到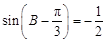 ,然后再结合正弦定理,得到关于角C的方程,求解角C,然后分析得到角B的值。
,然后再结合正弦定理,得到关于角C的方程,求解角C,然后分析得到角B的值。
解:(Ⅰ)∵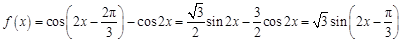 ,
,
∴.故函数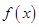 的最小正周期为
的最小正周期为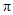 ;递增区间为
;递增区间为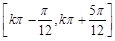 (
(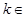 Z )………6分
Z )………6分
(Ⅱ)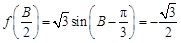 ,∴
,∴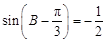 .
.
∵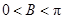 ,∴
,∴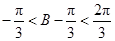 ,∴
,∴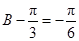 ,即
,即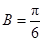 .…………………9分
.…………………9分
由正弦定理得: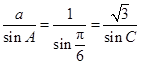 ,∴
,∴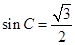 ,∵
,∵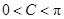 ,∴
,∴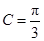 或
或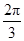 .
.
当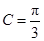 时,
时,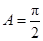 ;当
;当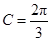 时,
时,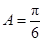 .(不合题意,舍)
.(不合题意,舍)
所以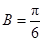 .
. 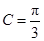 ……………………12分
……………………12分
(1)因为
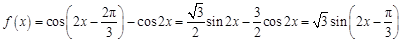 ,然后利用函数的周期公式和单调性得到结论。
,然后利用函数的周期公式和单调性得到结论。(2)根据上一问得到
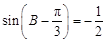 ,然后再结合正弦定理,得到关于角C的方程,求解角C,然后分析得到角B的值。
,然后再结合正弦定理,得到关于角C的方程,求解角C,然后分析得到角B的值。解:(Ⅰ)∵
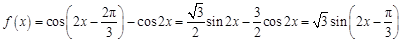 ,
,∴.故函数
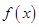 的最小正周期为
的最小正周期为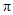 ;递增区间为
;递增区间为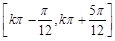 (
(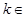 Z )………6分
Z )………6分(Ⅱ)
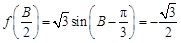 ,∴
,∴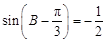 .
.∵
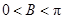 ,∴
,∴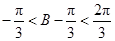 ,∴
,∴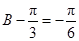 ,即
,即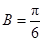 .…………………9分
.…………………9分由正弦定理得:
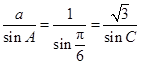 ,∴
,∴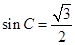 ,∵
,∵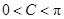 ,∴
,∴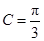 或
或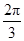 .
.当
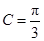 时,
时,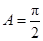 ;当
;当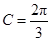 时,
时,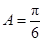 .(不合题意,舍)
.(不合题意,舍)所以
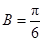 .
. 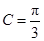 ……………………12分
……………………12分
练习册系列答案
相关题目
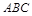 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. 的值域是( )
的值域是( ) cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R. sin2xcos2x是( )
sin2xcos2x是( ) 的奇函数
的奇函数 的奇函数
的奇函数 的图象关于点
的图象关于点 成中心对称,若
成中心对称,若 ,则
,则 __________ .
__________ .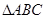 中,角
中,角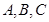 的对边分别为
的对边分别为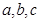 ,且
,且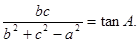
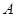 ;
;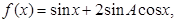 将函数
将函数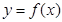 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的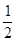 ,把所得图象向右平移
,把所得图象向右平移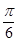 个单位,得到函数
个单位,得到函数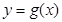 的图象,求函数
的图象,求函数 的最小正周期为
的最小正周期为 ,其中
,其中 ,则
,则 = .
= .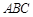 中,角A,B,C的对边分别为 a,b,c.且
中,角A,B,C的对边分别为 a,b,c.且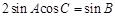 ,则
,则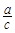
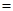 .
.