题目内容
n2(n≥4)个正数排成n行n列:a11,a12,a13,…,a1n
a21,a22,a23…,a2n
…………………
an1,an2,an3,…,ann
其中每一行的数成等差数列,每一列的数成等比数列,并且所有公比相等,已知a24=1,a42=![]() ,a43=
,a43=![]() .求a11+a22+…+ann.
.求a11+a22+…+ann.
思路解析:本题难度较大,须把an作为基数入手求出其他各需要的项. 解:设数列{a1k}的公差为d,数列{aik}(i=1,2,…,n)的公比为q,则 a1k=a11+(k-1)d, akk=[a11+(k-1)d]qk-1(为了计算akk,预先求出a11,d,q), 依题意,得 又∵n2个数都是正数,∴a11=d=q= 评注:本题很有新意:将等差数列和等比数列巧妙地结合在一起,不但考查了两种特殊数列的有关知识,还考查了数列求和——错项相减法.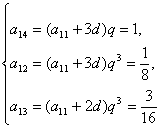
![]() a11=d=q=±
a11=d=q=±![]() .
.![]() .∴akk=
.∴akk=![]() .∴S=
.∴S=![]() +2×
+2×![]() +3×
+3×![]() +…+n×
+…+n×![]() .
.![]() S=
S=![]() +2×
+2×![]() +…+(n-1)×
+…+(n-1)×![]() +n×
+n×![]() ,两式相减,得S=2-
,两式相减,得S=2-![]() -
-![]() .
.
单元评价测试卷系列答案
学习与评价山东教育出版社系列答案
正大图书中考真题分类卷系列答案
5年中考试卷系列答案
大爱图书纵向解析与命题设计中考试题精选系列答案
首师金卷重点校中考模拟测试卷系列答案
赢在起跑线快乐寒假河北少年儿童出版社系列答案
春雨教育考必胜中考试卷精选系列答案
天利38套解锁中考真题档案系列答案
中考速递河南中考系列答案
 如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若
如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若 n2(n≥4)个正数排成n行n列:其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知a24=1,
n2(n≥4)个正数排成n行n列:其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知a24=1,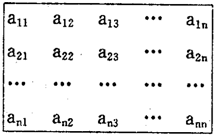 (2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32=
(2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32=