题目内容
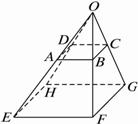
已知O、A、B、C、D、E、F、G、H为空间的9个点(如图)，并且
=k
,
=k
,
=k
,
=
+m
,
=
+m
.求证：(1)A、B、C、D四点共面，E、F、G、H四点共面；
(2)ＡC∥EG；
(3)OG=kOC.
证明:(1)由
=+m,=+m知A、B、C、D四点共面，E、F、G、H四点?共面?．?
(2)∵=+m
=-+m(-)?
=k(
-
)+km(
-
)?
=k
+km
=k(
+m
)=k
,?
∴
∥
.?
(3)由(2)知?
=
-
=k
-k
=k(
-
)=k
.
∴
=k
.
温馨提示：判断两向量a、b平行，就是判断a=λb是否成立，若成立则共线;若不成立则不共线．
练习册系列答案
相关题目
给出下列四个命题：已知O、A、B、C是不共线的四点，若存在一组正实数λ1﹑λ2﹑λ3，使λ1
+λ2
+λ3
=
，则三个角∠AOB、∠BOC、∠COA（ ）
| OA |
| OB |
| OC |
| 0 |
| A、都是锐角 |
| B、至多有两个钝角 |
| C、恰有两个钝角 |
| D、至少有两个钝角 |
；
，则α+β=1是A、B、C三点共线的充要条件；
（p为正常数，n∈N*），则称数列an是“等方比数列”．根据此定义可以断定：若数列an是“等方比数列”，则它一定是等比数列；
∥
;