题目内容
已知数列 的首项
的首项 ,且
,且 ,则
,则 为( )
为( )
| A.7 | B.15 | C.30 | D.31 |
D
解析试题分析:由 可知
可知 ,所以数列
,所以数列 是以2为首项,以2为公比的等比数列,所以
是以2为首项,以2为公比的等比数列,所以
考点:本小题主要考查数列递推关系的应用.
点评:本小题也可以依次计算求 ,但解析中由数列的递推关系式求通项公式的方法应用掌握,经常考查.
,但解析中由数列的递推关系式求通项公式的方法应用掌握,经常考查.

练习册系列答案
相关题目
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域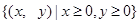 内植树,第一棵树在
内植树,第一棵树在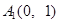 点,第二棵树在
点,第二棵树在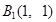 点,第三棵树在
点,第三棵树在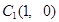 点,第四棵树在
点,第四棵树在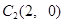 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )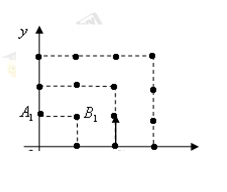
| A.(9,44) | B.(10,44) | C.(10.43) | D.(11,43) |
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A.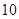 | B.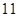 | C.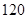 | D.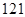 |
将石子摆成如图的梯形形状,称数列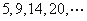 为“梯形数”.根据图形的构成,数列的第10项为( )
为“梯形数”.根据图形的构成,数列的第10项为( )


A.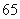 | B.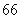 | C.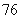 | D. |
已知数列 的通项公式为
的通项公式为 ,设其前
,设其前 项和为
项和为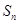 ,则使
,则使 成立的自然数
成立的自然数 有( )
有( )
| A.最大值31 | B.最小值31 | C.最大值63 | D.最小值63 |
若数列 中,
中, ,则
,则 取得最大值时
取得最大值时 的值是( )
的值是( )
| A. 13 | B. 14 | C. 15 | D. 14或15 |
已知
 则当
则当 时,n的最小值是
时,n的最小值是
| A.9 | B.10 | C.11 | D.12 |
 的值是( ).
的值是( ).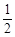

 ,定义Hn=
,定义Hn= 为
为 ,则数列
,则数列