题目内容
12.圆:x2+y2+cx+c2-c=0过原点的充要条件是c=1.分析 x2+y2+cx+c2-c=0过原点的充要条件是原点的坐标满足该方程.
解答 解:圆:x2+y2+cx+c2-c=0过原点的充要条件是 0+0+0+c2-c=0,
求得c2-c=0,即 c=1 或c=0(舍去),
故答案为:c=1.
点评 本题主要考查圆的一般方程,圆过原点的充要条件,属于基础题.

练习册系列答案
相关题目
2.某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为$\frac{1}{9}$,通过对被抽取学生的问卷调查,得到如下2x2列联表:
(I)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
(皿)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
| P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
3.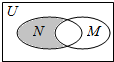 设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
 设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
20.已知集合M={x|x=$\frac{k}{5}+\frac{1}{10}$,k∈Z} N={x|$\frac{k}{10}+\frac{1}{5}$,k∈Z},则( )
| A. | M=N | B. | M⊆N | C. | M?N | D. | M∩N=Φ |
4.若x=-2是关于x的一元二次方程x2-$\frac{5}{2}$ax+a2=0的一个根,则a的值为( )
| A. | 1或4 | B. | -1或-4 | C. | -1或4 | D. | 1或-4 |