题目内容
已知函数 在点
在点 处的切线方程为
处的切线方程为 ,且对任意的
,且对任意的 ,
, 恒成立.
恒成立.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求实数 的最小值;
的最小值;
(Ⅲ)求证: (
( ).
).
 在点
在点 处的切线方程为
处的切线方程为 ,且对任意的
,且对任意的 ,
, 恒成立.
恒成立.(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)求实数
 的最小值;
的最小值;(Ⅲ)求证:
 (
( ).
).(Ⅰ) (Ⅱ)
(Ⅱ)
(Ⅲ)先证 ,累加即得.
,累加即得.
 (Ⅱ)
(Ⅱ)
(Ⅲ)先证
 ,累加即得.
,累加即得.试题分析:(Ⅰ)将
 代入直线方程得
代入直线方程得 ,∴
,∴ ①
①  ,∴
,∴ ②
② 联立,解得
 ∴
∴
(Ⅱ)
 ,∴
,∴ 在
在 上恒成立;
上恒成立;即
 在
在 恒成立;
恒成立; 设
 ,
, ,
,∴只需证对于任意的
 有
有

设
 ,
,1)当
 ,即
,即 时,
时, ,∴
,∴
 在
在 单调递增,∴
单调递增,∴
2)当
 ,即
,即 时,设
时,设 是方程
是方程 的两根且
的两根且
由
 ,可知
,可知 ,分析题意可知当
,分析题意可知当 时对任意
时对任意 有
有 ;
;∴
 ,∴
,∴
综上分析,实数
 的最小值为
的最小值为 .
. (Ⅲ)令
 ,有
,有 即
即 在
在 恒成立;
恒成立;令
 ,得
,得

∴原不等式得证.
点评:本题考查了利用导数研究函数的切线方程问题,在曲线上某点处的切线的斜率就是该点的导数值,考查了导数在最大值和最小值中的应用,体现了数学转化思想和分类讨论的数学思想.特别是(Ⅲ)的证明,用到了放缩法和裂项相消,此题属难度较大的题目.

练习册系列答案
相关题目
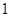 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度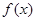 与时间
与时间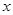 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: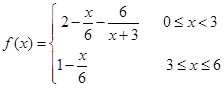 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于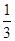 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.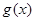 ,求
,求 ,
, .
. ,求
,求 的取值范围;
的取值范围; 的解集为R,求
的解集为R,求 的取值范围.
的取值范围. .若关于
.若关于 的不等式
的不等式 的解集非空,则实数
的解集非空,则实数 的取值范围是________.
的取值范围是________. 是方程
是方程 的解,则
的解,则 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:



 的两个实根一个小于?1,另一个大于1,那么实数m的取值范围是( )
的两个实根一个小于?1,另一个大于1,那么实数m的取值范围是( )