题目内容
探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
函数f(x)=x+ (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;
(1)函数f(x)=x+ (x>0)在区间 上递增.
(x>0)在区间 上递增.
当x= 时,y最小= .
(2)证明:函数f(x)=x+ 在区间(0,2)上递减.
在区间(0,2)上递减.
(3)思考:函数f(x)=x+ (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)(1)(2,+∞);2;4(2)证明如下(3)当x=-2时,有最大值-4
试题分析:(1)(2,+∞);2;4
(2)任取
 ∈(0, 2)且
∈(0, 2)且 于是,f(
于是,f( )-f(
)-f( )
)=(x
 +
+ )-(x2+
)-(x2+ ) =
) =
(1)∵ x
 , x
, x ∈(0, 2) 且 x
∈(0, 2) 且 x <x
<x
∴ x
 -x
-x <0;x
<0;x x
x -4<0; x
-4<0; x x
x >0
>0∴(1)式>0 即f(x
 )-f(x
)-f(x )>0,f(x
)>0,f(x )>f(x
)>f(x )
)∴f(x)在区间(0, 2)递减. 10分
(3)当x=-2时,有最大值-4提示:f(x)在(-∞,0)∪(0, ∞)
为奇函数.图象关于原点对称.
点评:证明函数
 在区间
在区间 上为增(减)函数的方法是:令
上为增(减)函数的方法是:令 ,若
,若
(
 ),则函数为增(减)函数。
),则函数为增(减)函数。
练习册系列答案
相关题目
 的值为 .
的值为 .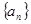 中,
中,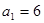 ,点
,点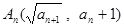 在抛物线
在抛物线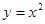 上;数列
上;数列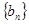 中,点
中,点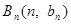 在过点(0, 1),以
在过点(0, 1),以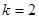 为斜率的直线上。
为斜率的直线上。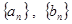 的通项公式;
的通项公式; 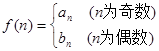 , 问是否存在
, 问是否存在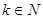 ,使
,使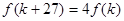 成立,若存在,求出
成立,若存在,求出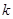 值;若不存在,说明理由;
值;若不存在,说明理由;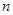 ,不等式
,不等式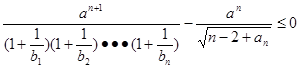 恒成立,求正数
恒成立,求正数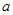 的取值范围。
的取值范围。 符号
符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )



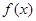 是R上的偶函数,且在
是R上的偶函数,且在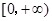 上单调递增,则
上单调递增,则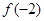 ,
,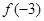 ,
, 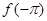 的大小顺序是:( )
的大小顺序是:( )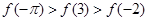
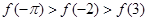
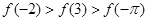
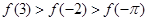
 在点
在点 处的切线方程为
处的切线方程为 ,且对任意的
,且对任意的 ,
, 恒成立.
恒成立. 的解析式;
的解析式; 的最小值;
的最小值; (
( ).
).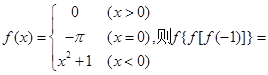
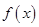 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足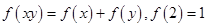 .
.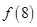 的值; (2)求不等式
的值; (2)求不等式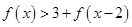 的解集.
的解集.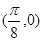 为函数
为函数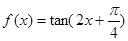 的一个对称中心
的一个对称中心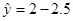 x,当变量x增加一个单位时,y大约减少2.5个单位
x,当变量x增加一个单位时,y大约减少2.5个单位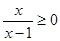 ”则
”则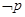 “
“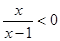 ”
”