题目内容
凸函数的性质定理为:如![]() 果函数f(x)在区间D上是凸函数,则对D内的任意x1,x2,…,xn都有
果函数f(x)在区间D上是凸函数,则对D内的任意x1,x2,…,xn都有![]() ≤f(
≤f(![]() ).已知函数f(x)=sinx在(0,π)上是凸函数,则
).已知函数f(x)=sinx在(0,π)上是凸函数,则
(1)求△ABC中,sinA+sinB+sinC的最大值.
(2)判断f(x)=2x在R上是否为凸函数.
(1)∵f(x)=sinx在(0![]() ,π)上是凸函数,A、B、C∈(0,π)且A+B+C=π,
,π)上是凸函数,A、B、C∈(0,π)且A+B+C=π,
∴![]() ≤f(
≤f(![]() )=f(
)=f(![]() ),
),
即sinA+sinB+sinC≤3sin![]() =
=![]() .
.
所以sinA+sinB+sinC的最大值为![]() .
.
(2)∵f(-1)=![]() ,f(1)=2,
,f(1)=2,
而![]() =
=![]() =
=![]() ,
,
而f(![]() )=f(0)=1,
)=f(0)=1,
∴![]() >f(
>f(![]() ).
).
即不满足凸函数的性质定理,故f(x)=2x不是凸函数.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
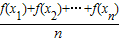 ≤f(
≤f(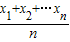 ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为 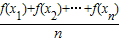 ≤f(
≤f(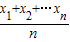 ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为 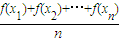 ≤f(
≤f(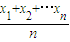 ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为