题目内容
选修4-1:几何证明选讲
如图,直线 经过⊙
经过⊙ 上一点
上一点 ,⊙
,⊙ 的半径为
的半径为 ,
, 是等腰三角形,且
是等腰三角形,且 是
是 中点,⊙
中点,⊙ 交直线
交直线 于
于 .
.

(Ⅰ)证明:直线 与⊙
与⊙ 相切;
相切;
(Ⅱ)若 的正切值为
的正切值为 ,求
,求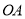 的长.
的长.
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
题目内容
选修4-1:几何证明选讲
如图,直线 经过⊙
经过⊙ 上一点
上一点 ,⊙
,⊙ 的半径为
的半径为 ,
, 是等腰三角形,且
是等腰三角形,且 是
是 中点,⊙
中点,⊙ 交直线
交直线 于
于 .
.

(Ⅰ)证明:直线 与⊙
与⊙ 相切;
相切;
(Ⅱ)若 的正切值为
的正切值为 ,求
,求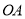 的长.
的长.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案