Question

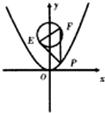曲线C₁：x²+（y-4）²=1，曲线C₂：x²=2y，EF是曲线C₁的任意一条直径，P是曲线C₂上任一点，则

PE

•

PF

的最小值为（　　）

A．5

B．6

C．7

D．8

Answer 1

分析：①当EF的斜率不存在时，对于曲线C₁：x²+（y-4）²=1，令x=0，解得点E，F的坐标．设P(m，

m2

2

)，利用

PE

•

PF

及二次函数的单调性即可得出．
②当EF的斜率存在时，设直线EF的斜率为k，则方程为y=kx+4．与圆的方程联立解得点E，F的坐标．设P(m，

m2

2

)，即可得出

PE

•

PF

，利用二次函数的单调性即可得出．

解答：解：①当EF的斜率不存在时，对于曲线C₁：x²+（y-4）²=1，令x=0，得（y-4）²=1，解得y=3或5．
取E（0，3），F（0，5），设P(m，

m2

2

)，则

PE

•

PF

=(-m，3-

m2

2

)•(-m，5-

m2

2

)=m2+(3-

m2

2

)(5-

m2

2

)=

1

4

(m2-6)2+6≥6，当且仅当m²=6，即m=±

6

时取等号．
此时P(±

6

，3)．
②当EF的斜率存在时，设直线EF的斜率为k，则方程为y=kx+4．
联立

y=kx+4 x2+(y-4)2=1

，化为x2=

1

1+k2

，
取E(-

1 1+k2

，-k•

1 1+k2

+4)，F(

1 1+k2

，k•

1 1+k2

+4)．
设P(m，

m2

2

)．
则

PE

•

PF

=(-

1 1+k2

-m，-k

1 1+k2

+4-

m2

2

)•(

1 1+k2

-m，k

1 1+k2

+4-

m2

2

)
=m2-

1

1+k2

+(4-

m2

2

)2-

k2

1+k2

=

1

4

(m2-6)2+6≥6．当且仅当m²=6，即m=±

6

时取等号．
此时P(±

6

，3)．
综上可知：

PE

•

PF

的最小值为6．
故选B．

点评：本题考查了直线与圆相交转化为方程联立得到方程组、抛物线的标准方程、分类讨论、向量的数量积运算、二次函数的单调性等基础知识与基本技能方法，属于难题．