题目内容

直线方程为cosα•x+sinα•y+2=0，α∈（
π
2
，π），则直线的倾斜角为（　　）
分析：求出直线的斜率，根据斜率与倾斜角的关系可得结论．
解答：解：直线方程为cosα•x+sinα•y+2=0的斜率为-
cosα
sinα
=tan（α-
π
2
），
∵α∈（
π
2
，π），
∴α-
π
2
∈（0，
π
2
），
∴直线的倾斜角为α-
π
2
，
故选B．
点评：本题考查直线的斜率，正确运用斜率与倾斜角的关系是关键．
练习册系列答案
相关题目
已知在平面直角坐标系xoy中，圆C的参数方程为
x=
3
+3cosθ
y=1+3sinθ
（θ为参数），以ox为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
6
)=0则圆C截直线l所得的弦长为
4
2
4
2
．
A．选修4-1：几何证明选讲
如图，直角△ABC中，∠B=90°，以BC为直径的⊙O交AC于点D，点E是AB的中点．
求证：DE是⊙O的切线．
B．选修4-2：矩阵与变换
已知二阶矩阵A有特征值-1及其对应的一个特征向量为
1
-4
，点P（2，-1）在矩阵A对应的变换下得到点P′（5，1），求矩阵A．
C．选修4-4：坐标系与参数方程
在直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρcos(θ-
π
4
)=
2
，曲线C的参数方程为
x=2cosα
y=sinα
（α为参数），求曲线C截直线l所得的弦长．
D．选修4-5：不等式选讲
已知a，b，c都是正数，且abc=8，求证：log2（2+a）+log2（2+b）+log2（2+c）≥6．
（2011•崇明县二模）已知直线l的极坐标方程为ρcos（θ-
π
4
）=
2
2
，则极点到这条直线的距离等于
2
2
2
2
．
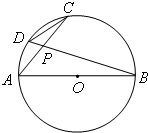（2007•深圳一模）请从下面两题中选做一题，如果两题都做，以第一题的得分为最后得分．
（1）在极坐标系中，过圆ρ=4cosθ的圆心，且垂直于极轴的直线方程为
ρcosθ=2
ρcosθ=2
．
（2）如图，AB为⊙O的直径，弦AC、BD交于点P，若AB=3，CD=1，则sin∠APD=
2
2
3
2
2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网