题目内容
在△ABC中，C为钝角，| AB |
| BC |
| 3 |
| 2 |
| 1 |
| 3 |
分析：先根据正弦定理求得sinC的值，进而求得C，进而根据sinB=sin（A+C）利用两角和公式求得答案．
解答：解：由正弦定理可知
=
∴sinC=
sinA=
∵C为钝角，
∴C=150°
cosA=
=
∴sinB=sin（A+C）=-
×
+
×
=
故答案为150°，
| AB |
| BC |
| sinC |
| sinA |
∴sinC=
| AB |
| BC |
| 1 |
| 2 |
∵C为钝角，
∴C=150°
cosA=
1-
|
2
| ||
| 3 |
∴sinB=sin（A+C）=-
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||||
| 6 |
故答案为150°，
2
| ||||
| 6 |
点评：本题主要考查了正弦定理，同角三角函数基本关系的应用，和利用两角和公式化简求值．考查了学生分析问题和基本的运算能力．
练习册系列答案
相关题目
+
•
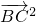=0，则△ABC的形状是
+
•
=0，则△ABC的形状是（ ）