题目内容
14.对于函数y=g(x),部分x与y的对应关系如下表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 2 | 4 | 7 | 5 | 1 | 8 |
| A. | 4054 | B. | 5046 | C. | 5075 | D. | 6047 |
分析 由题意易得数列是周期为4的周期数列,可得x1+x2+…+x2015=503(x1+x2+x3+x4)+x1+x2+x3,代值计算可得.
解答 解:∵数列{x n }满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=g(x)的图象上,∴xn+1=g(xn),
∴由图表可得x1=2,x2=f(x1)=4,x3=f(x2)=5,x4=f(x3)=1,x5=f(x4)=2,
∴数列是周期为4的周期数列,故 x1+x2+…+x2015=503(x1+x2+x3+x4)+x1+x2+x3=503×(2+4+5+1)+2+4+5=6047,
故选:D.
点评 本题考查函数和数列的关系,涉及周期性问题,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
4.式子$\frac{lo{g}_{8}27}{lo{g}_{2}3}$的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |
2.设集合A={x|1≤x≤6,x∈N},对于A的每个非空子集,定义其“交替和”如下:把集合中的数按从大到小的顺序排列,然后从最大的数开始交替地加减各数(如:{1,2,5}的“交替和”是5-2+1=4,{6,3}的“交替和”就是6-3=3,{3}的“交替和”就是3).则集合A的所有这些“交替和”的总和为( )
| A. | 128 | B. | 192 | C. | 224 | D. | 256 |
19.函数f(x)=x2+lnx的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.圆x2+y2-2x-5=0与圆x2+y2+2x-4y-4=0的交点为A,B,则线段AB的垂直平分线的方程是( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | x-2y+1=0 | D. | x-y+1=0 |
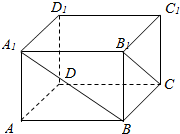 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.