题目内容
已知曲线C上的动点P( )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为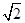
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。
(1): (或
(或 );(2)
);(2) 或
或
解析试题分析:(1)根据动点P(x,y)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比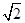 ,建立方程,化简可得曲线C的方程.
,建立方程,化简可得曲线C的方程.
(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线l的方程.
试题解析:(1)由题意得|PA|=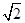 |PB| 2分;
|PB| 2分;
故 3分;
3分;
化简得: (或
(或 )即为所求。 5分;
)即为所求。 5分;
(2)当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 ,
,
将 代入方程
代入方程 得
得 ,
,
所以|MN|=4,满足题意。 8分;
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 +2
+2
由圆心到直线的距离 10分;
10分;
解得 ,此时直线
,此时直线 的方程为
的方程为
综上所述,满足题意的直线 的方程为:
的方程为: 或
或 。 12分.
。 12分.
考点:(1)圆的标准方程;(2)点到直线的距离公式.

练习册系列答案
相关题目
 轴所得弦长为
轴所得弦长为 ;②被
;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线 :
: 的距离为
的距离为 的圆的方程。
的圆的方程。 和直线
和直线 所得弦长分别为
所得弦长分别为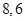 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。
 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点. 与直线
与直线 相切且与圆
相切且与圆 :
: 外切。
外切。 方程;
方程; 作直线
作直线 交轨迹
交轨迹 两点,
两点, 是
是 点关于坐标原点
点关于坐标原点 的对称点,求证:
的对称点,求证: ;
; :
: 和圆
和圆 :
:

 ,求直线l的方程;
,求直线l的方程; 和
和 ,它们分别与圆
,它们分别与圆 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点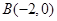 的动直线
的动直线 与圆
与圆 相交于
相交于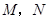 两点,
两点, 是
是 的中点,直线
的中点,直线 相交于点
相交于点 .
.
 时,求直线
时,求直线 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.