题目内容
一动圆截直线 和直线
和直线 所得弦长分别为
所得弦长分别为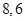 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。
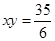
解析试题分析:设动圆圆心为M,由动圆截两直线所得的弦长,结合点到直线的距离公式,根据半径相等列关于动圆圆心坐标的关系式,整理后得答案.
试题解析:设动圆圆心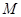 点的坐标为
点的坐标为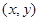 ,
,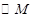 分别截直线
分别截直线 和
和 所得弦分别为
所得弦分别为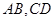 ,则
,则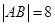 ,
,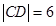 ,过
,过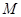 分别作直线
分别作直线 和
和 的垂线,垂足分别为
的垂线,垂足分别为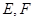 ,则
,则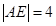 ,
,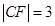 ,
,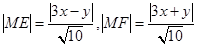 ,
,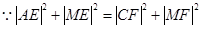 ,
, 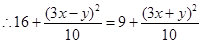 ,
, 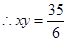 ,所以动圆圆心的轨迹方程是
,所以动圆圆心的轨迹方程是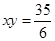 .
.
考点:轨迹方程.

练习册系列答案
相关题目
题目内容
一动圆截直线 和直线
和直线 所得弦长分别为
所得弦长分别为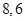 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。
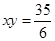
解析试题分析:设动圆圆心为M,由动圆截两直线所得的弦长,结合点到直线的距离公式,根据半径相等列关于动圆圆心坐标的关系式,整理后得答案.
试题解析:设动圆圆心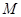 点的坐标为
点的坐标为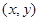 ,
,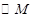 分别截直线
分别截直线 和
和 所得弦分别为
所得弦分别为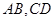 ,则
,则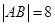 ,
,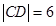 ,过
,过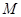 分别作直线
分别作直线 和
和 的垂线,垂足分别为
的垂线,垂足分别为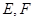 ,则
,则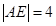 ,
,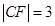 ,
,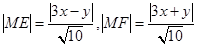 ,
,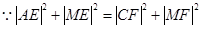 ,
, 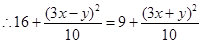 ,
, 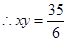 ,所以动圆圆心的轨迹方程是
,所以动圆圆心的轨迹方程是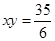 .
.
考点:轨迹方程.
