题目内容
已知圆满足:①截 轴所得弦长为
轴所得弦长为 ;②被
;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线 :
: 的距离为
的距离为 的圆的方程。
的圆的方程。
 或
或
解析
试题分析:依题意,可设所求圆心为 ,半径为
,半径为 ,由①截
,由①截 轴所得的弦长为2可得
轴所得的弦长为2可得 ;由②被x轴分成两段圆弧,其弧长的比为3:1可知劣弧所对的圆心角为90°,从而有
;由②被x轴分成两段圆弧,其弧长的比为3:1可知劣弧所对的圆心角为90°,从而有 ;再由③圆心到直线
;再由③圆心到直线 :
: 的距离为
的距离为 可得
可得 ,综合可求得
,综合可求得 的值,从而可得该圆的方程.
的值,从而可得该圆的方程.
试题解析:解:设
当 时,
时, ∵
∵ ∴
∴
∴

∴ ①
①
当 时,
时, ∵
∵
∴ ∴
∴ ②
②
由①、②得: 又∵
又∵ 到
到 的
的
∴ ∴
∴ ∴
∴ 或
或
∴ 或
或 ∴
∴ 或
或

∴ 或
或
考点:1.圆的标准方程;2.直线与圆的位置关系.

练习册系列答案
相关题目
 与直线
与直线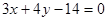 相切于点
相切于点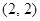 ,其圆心在直线
,其圆心在直线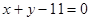 上,求圆
上,求圆 +y2=1.过
+y2=1.过 轴上的动点
轴上的动点 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点. 的最大距离;
的最大距离;  时,求A,B两点坐标;
时,求A,B两点坐标; 与圆
与圆 交于
交于 两点,以
两点,以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆 两点,延长
两点,延长 交圆
交圆 ,延长
,延长 交圆
交圆 .已知
.已知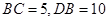 .
.
 的长;
的长; .
. 是椭圆
是椭圆 上两点,点M的坐标为
上两点,点M的坐标为 .
. 轴对称,且
轴对称,且 为等边三角形时,求
为等边三角形时,求 的长;
的长; :
: ,点
,点 ,直线
,直线 .
.
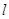 垂直的直线方程;
垂直的直线方程; 上(
上( 为坐标原点),存在定点
为坐标原点),存在定点 (不同于点
(不同于点 ),满足:对于圆
),满足:对于圆 ,都有
,都有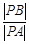 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.
 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为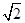
 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。