Question

求适合下列条件的双曲线的标准方程.

（1）a=2,经过点A（2，-5）焦点在y轴上;

(2)a=b，经过点（3，-1）.

Answer 1

分析：首先要确定是哪种形式的标准方程，然后利用待定系数法确定相应的参数.

解：（1）焦点在y轴上的双曲线设为=1,（a＞0,b＞0）

由a=2，且点A（2，-5）在双曲线上得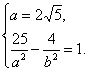

解得b²=16,因此，所求的双曲线标准方程为=1.

（2）当焦点在x轴上时，可设双曲线方程为x²-y²=a²,将点（3，-1）代入得9-1=a²，所以a²=b²=8，因此，所求的双曲线标准方程为=1;当焦点在y轴上时，可设双曲线方程为y²-x²=a²，将点（3，-1）代入得1-9=a²，a²=-8不可能.综上所求的双曲线标准方程为=1.

点拨：利用待定系数法求双曲线的标准方程是此类问题的典型解法，注意讨论焦点的位置，不要漏解，对焦点不确定的情况可设为=1,(mn＜0)以避免讨论.