题目内容
己知f(x)在(-1,1)上有定义,f(
)=-1,且满足x.,y∈(-1,1)有f(x)+f(y)=f(
).
(I)判断为f(x)在(-1,1)上的奇偶性:
(II)对数列x1=
,xn+1=
,求f(xn)
(111)求证:
+
+…+
>-
.
| 1 |
| 2 |
| x+y |
| 1-xy |
(I)判断为f(x)在(-1,1)上的奇偶性:
(II)对数列x1=
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
(111)求证:
| 1 |
| f(x1) |
| 1 |
| fx2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |
分析:(I)利用赋值法,先求得f(0)=0,再令y=-x,即可得到f(x)为奇函数;
(II)先确定f(x1)=f(
)=-1,利用xn+1=
,根据f(x)+f(y)=f(
),可得{f(xn)}是以-1为首项,2为公比的等比数列,从而可求f(xn);
(III)证明
+
+…+
>-2,
=<-2,即可得到结论.
(II)先确定f(x1)=f(
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
| x+y |
| 1-xy |
(III)证明
| 1 |
| f(x1) |
| 1 |
| fx2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |
解答:(I)解:令x=y=0,则2f(0)=f(0),所以f(0)=0
令y=-x,则f(x)+f(-x)=f(0)=0
所以f(-x)=-f(x)
所以f(x)为奇函数;
(II)解:∵x1=
,∴f(x1)=f(
)=-1,
∵xn+1=
,∴f(xn+1)=f(
)=f(xn)+f(xn)=2f(xn)
∴
=2
∴{f(xn)}是以-1为首项,2为公比的等比数列
∴f(xn)=-2n-1;
(III)证明:∵
+
+…+
=-(1+
+…+
)=-(2-
)>-2
而
=-(2+
)<-2
∴
+
+…+
>-
.
令y=-x,则f(x)+f(-x)=f(0)=0
所以f(-x)=-f(x)
所以f(x)为奇函数;
(II)解:∵x1=
| 1 |
| 2 |
| 1 |
| 2 |
∵xn+1=
| 2xn |
| 1+xn2 |
| 2xn |
| 1+xn2 |
∴
| f(xn+1) |
| f(xn) |
∴{f(xn)}是以-1为首项,2为公比的等比数列
∴f(xn)=-2n-1;
(III)证明:∵
| 1 |
| f(x1) |
| 1 |
| fx2) |
| 1 |
| f(xn) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
而
| 2n+5 |
| n+2 |
| 1 |
| n+2 |
∴
| 1 |
| f(x1) |
| 1 |
| fx2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |
点评:本题考查赋值法的运用,考查等比数列的证明,考查不等式的证明,确定数列为等比数列是关键.

练习册系列答案
相关题目
 )=-1,且满足x.,y∈(-1,1)有f(x)+f(y)=
)=-1,且满足x.,y∈(-1,1)有f(x)+f(y)= .
. ,求f(xn)
,求f(xn)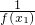 +
+ +…+
+…+ >-
>- .
.