题目内容

2．若函数y=（m-2）2（m+1）x在（-∞，+∞）上是减函数，求实数m的取值范围．

分析 根据复合函数单调性之间的关系进行判断求解即可．

解答 解：若y=（m-2）2（m+1）x在（-∞，+∞）上是减函数，
则满足$\left\{\begin{array}{l}{m-2＞0}\\{m+1＜0}\end{array}\right.$或$\left\{\begin{array}{l}{m-2＜0}\\{m+1＞0}\end{array}\right.$，
即$\left\{\begin{array}{l}{m＞2}\\{m＜-1}\end{array}\right.$或$\left\{\begin{array}{l}{m＜2}\\{m＞-1}\end{array}\right.$，
解得-1＜m＜2，
即实数m的取值范围是（-1，2）．

点评 本题主要考查函数单调性的应用，根据复合函数单调性之间的关系是解决本题的关键．

练习册系列答案
相关题目
12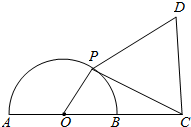．如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（　　）
A．2B．$\frac{5\sqrt{3}}{4}$-2C．$\frac{5\sqrt{3}}{4}$D．2+$\frac{5\sqrt{3}}{4}$
13．已知x＞$\frac{1}{2}$，当$\frac{2{x}^{2}-x+1}{2x-1}$取最小值时，x值是$\frac{\sqrt{2}+1}{2}$．
10．求下列函数的值域：
（1）y=-x2+2x+3；
（2）y=-x2+2x+3，x∈[0，3）；
（3）y=-x2+2x+3，x∈（1，3）；
（4）y=-x2+2x+3，x∈（-3，$\frac{1}{2}$]；
（5）y=-x2+2x+3，x∈（-2，+∞）．
17．若a=2，b＞0，$\frac{a^2b+{a}^{\frac{1}{2}}}{{a}^{\frac{1}{2}}b}$+（${a}^{\frac{1}{2}}$-${b}^{-\frac{1}{3}}$）（a+${a}^{\frac{1}{2}}$${b}^{-\frac{1}{3}}$+${b}^{-\frac{2}{3}}$）的值．
7．据某校环保小组调查，某区垃圾量的年增长率为m，2010年产生的垃圾量为a吨，由此预测，该区2015年产生的垃圾量为a（1+m）5吨．
14．当a=$\sqrt{3}$+$\sqrt{2}$，b=-$\frac{27}{8}$时，求代数式$\frac{{a}^{\frac{2}{3}}-{b}^{-\frac{2}{3}}}{{a}^{\frac{1}{3}}+{b}^{-\frac{1}{3}}}$-$\frac{a+{b}^{-1}}{{a}^{\frac{2}{3}}-{a}^{\frac{1}{3}}{b}^{-\frac{1}{3}}+{b}^{-\frac{2}{3}}}$的值．
11．计算下列各式的值：
（1）$\root{n}{（3-π）^{n}}$（n＞1，且n∈N*）；
（2）$\root{2n}{（x-y）^{2n}}$（n＞1，且n∈N*）．
12．已知f（x）=$\frac{{x}^{2}+（a-b-2）x+1}{{x}^{2}+2}$是[b-1，a]上的偶函数，求f（a-b）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网