Question

12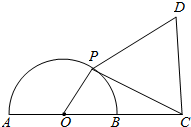．如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（　　）

• A． 2
• B． $\frac{5\sqrt{3}}{4}$-2
• C． $\frac{5\sqrt{3}}{4}$
• D． 2+$\frac{5\sqrt{3}}{4}$

Answer 1

分析 首先，可以设∠POB=θ，四边形面积为y，然后，建立关系式，构造面积关系式，最后利用三角函数知识求解最值．

解答 解：设∠POB=θ，四边形面积为y，
则在△POC中，由余弦定理得
PC²=OP²+OC²-2OP•OCcosθ=5-4cosθ．
∴y=S_△OPC+S_△PCD=$\frac{1}{2}$×1×2sinθ+$\frac{\sqrt{3}}{4}$（5-4cosθ）
=2sin（θ-$\frac{π}{3}$）+$\frac{5\sqrt{3}}{4}$，
当θ-$\frac{π}{3}$=$\frac{π}{2}$时，θ=$\frac{5π}{6}$，y有最大值为2+$\frac{5\sqrt{3}}{4}$．
故选：D．

点评 本题重点考查了三角函数的辅助角公式、三角恒等变换等知识，属于中档题．