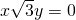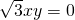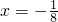题目内容
若方程a(b-c)x2+b(c-a)x+c(a-b)=0有等根,求证:
成等差数列.
证明:∵方程有等根,
∴Δ=b2(c-a)2-4a(b-c)c(a-b)=0,
即［b(a+c)-2ac］2=0.
∴b(a+c)=2ac,
即+
=
.
故
、
、
成等差数列.
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
（1）画出销售额和利润额的散点图．
（2）若销售额和利润额具有相关关系，用最小二乘法计算利润额y对销售额x的回归直线方程y=bx+a，其中b=
，a=
-b
．
（3）若获得利润是4.5时估计销售额是多少（百万）？
| 商店名称 | A | B | C | D | E |
| 销售额（x）/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额（y）/百万元 | 2 | 3 | 3 | 4 | 5 |
（2）若销售额和利润额具有相关关系，用最小二乘法计算利润额y对销售额x的回归直线方程y=bx+a，其中b=
| |||||||
|
. |
| y |
. |
| x |
（3）若获得利润是4.5时估计销售额是多少（百万）？
与抛物线y2=8x有一个公共的焦点F，且两曲线的一个交点为P，若|PF|=5，则双曲线的渐近线方程为
