题目内容
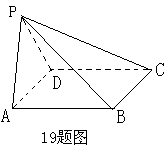 四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD
四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD![]() 底面ABCD,当
底面ABCD,当![]() 的值等于多少时,能使PB
的值等于多少时,能使PB![]() AC?并给出证明.
AC?并给出证明.
![]() =
=![]() 时,能使PB
时,能使PB![]() AC
AC
解析:
当![]() =
=![]() 时,能使PB
时,能使PB![]() AC
AC
证明:取AD中点F,连接PF,
![]() PF
PF![]() AD,面PAD
AD,面PAD![]() 面ABCD,
面ABCD,
![]() PF
PF![]() 面ABCD,
面ABCD,
连结BF,交AC于O,则根据题意,当![]() =
=![]() 时,有
时,有
AC=![]() AB,AF=
AB,AF=![]() AB,A
AB,A![]() O=
O=![]() AB,FO=
AB,FO=![]() AB.
AB.
∴AF2=AO2+FO2,即FB![]() AC,
AC,
由三垂线定理可证得PB![]() AC.
AC.
∴当![]() =
=![]() 时,能使PB
时,能使PB![]() AC.
AC.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
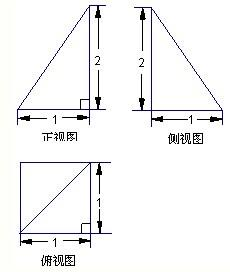 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
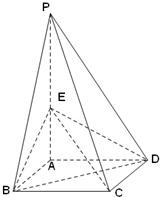 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: