题目内容
(本小题满分12分)
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:

(Ⅰ)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1)应选择学生乙参加知识竞赛.,(2)
【解析】
试题分析:根据茎叶图中的数据甲 、乙的平均成绩,如果相等则要再计算二者的方差,比较方差大小,方差较小者成绩稳定,就选取谁去参加比赛;第二步从学生甲的6次培训成绩中随机选择2个,选到的分数超过87分的个数为 ,则
,则 可取值有0,1,2,求出对应的概率值,
可取值有0,1,2,求出对应的概率值, ,同理求出:
,同理求出:
 ,
, ,列出概率分布列,求出数学期望即可.
,列出概率分布列,求出数学期望即可.
试题解析:(Ⅰ)学生甲的平均成绩 ,
,
学生乙的平均成绩 ,
,
又 ,
,
 ,
,
则 ,
, ,
,
说明甲、乙的平均水平一样,但乙的方差小,则乙发挥更稳定,故应选择学生乙参加知识竞赛.
(Ⅱ) 的所有可能取值为0,1,2,则
的所有可能取值为0,1,2,则
 ,
, ,
, ,
,
 的分布列为
的分布列为
| 0 | 1 | 2 |
P |
|
|
|
所以数学期望 .
.
考点:1.茎叶图;2.离散型随机变量的数学期望和方差

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



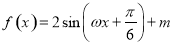 (其中
(其中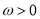 )的图像过点
)的图像过点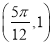 ,且其相邻两条对称轴之间的距离为
,且其相邻两条对称轴之间的距离为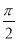 ,
,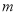 的值及
的值及 的单调递增区间;
的单调递增区间;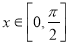 ,求
,求 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
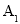 、
、 、
、 、
、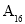 ,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )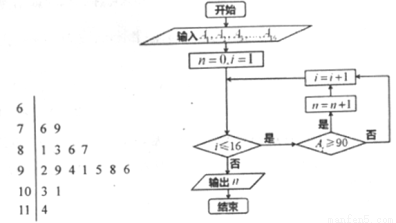
 B.
B. C.
C.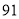 D.
D.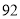
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则无穷数列
,则无穷数列 前
前 项和的极限为 .
项和的极限为 .  的直线与圆
的直线与圆 有公共点,则该直线的倾斜角的取值范围是
有公共点,则该直线的倾斜角的取值范围是 B.
B.  C.
C.  D.
D. 