题目内容
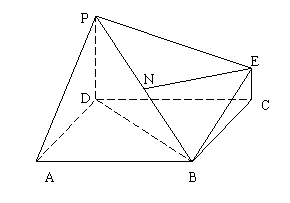
（12分）右图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC//PD，且PD＝AD＝2CE＝2 .
（1）若N为线段PB的中点，求证：EN⊥平面PDB；
（2）求该几何体的体积；
 |
（12分）
（1）证明：连结AC与BD交于点F, 连结NF，
∵F为BD的中点，N为PB的中点
∴NF//PD且NF＝
PD
又EC//PD且EC＝PD
∴NF//EC且NF＝EC
∴四边形NFCE为平行四边形
∴NE//FC
∵PD⊥平面ABCD，，AC
平面ABCD
∴PD⊥AC， ∵AC⊥BD且PD∩BD=D
∴AC⊥平面PBD ∵EN//AC
∴NE⊥平面PBD
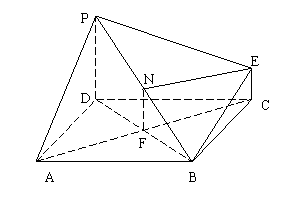（2）∵PD⊥平面ABCD，，BC平面ABCD
∴PD⊥BC，
∵BC⊥CD，平面PDCE∩平面DBC＝CD ∴BC⊥平面PDCE
∵
∴四棱锥B－CEPD的体积
∵三棱锥P－ABD的体积
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
平面
，
，且
=2 .
平面
． 
4分）右图为一简单组合体，其底面
为正方形，
平面
，
平面
与平面
所成角的
大小。
为正方形，
平面
，
平面
；（2）求
与平面
所成角的大小．
为正方形，
平面
//
。
//平面
；
为线段
的中点，
；
，求平面
与平面
平面
，
，且
=2 .
