题目内容
已知函数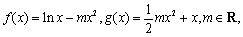 令
令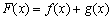 .
.
(Ⅰ)当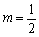 时,求函数
时,求函数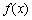 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于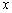 的不等式
的不等式 恒成立,求整数
恒成立,求整数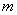 的最小值;
的最小值;
(Ⅲ)若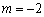 ,正实数
,正实数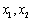 满足
满足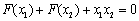 ,证明:
,证明: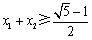 .
.
(Ⅰ)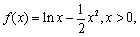
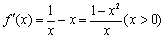
由 得
得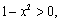 又
又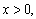 所以
所以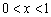 .所以
.所以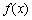 的单增区间为
的单增区间为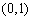 .
.
(Ⅱ)方法一:令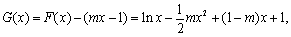
所以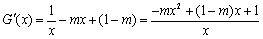 .
.
当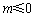 时,因为
时,因为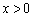 ,所以
,所以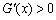 ,所以
,所以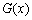 在
在 上是递增函数,
上是递增函数,
又因为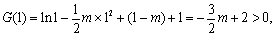 所以关于
所以关于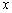 的不等式
的不等式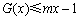 不能恒成立.
不能恒成立.
当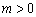 时,
时,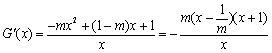 .
.
令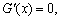 得
得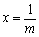 ,所以当
,所以当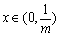 时,
时,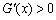 ;当
;当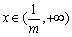 时,
时,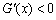 .
.
因此函数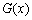 在
在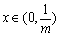 是增函数,在
是增函数,在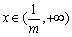 是减函数.
是减函数. 
故函数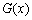 的最大值为
的最大值为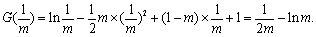 …………8分
…………8分
令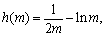 因为
因为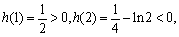
又因为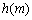 在
在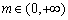 上是减函数,所以当
上是减函数,所以当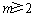 时,
时,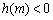 .
.
所以整数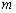 的最小值为. ……………10分
的最小值为. ……………10分
方法二:(2)由 恒成立,得
恒成立,得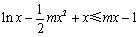 在
在 上恒成立.
上恒成立.
问题等价于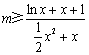 在
在 上恒成立.
上恒成立.
令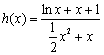 ,只要
,只要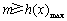 . ……………………6分
. ……………………6分
因为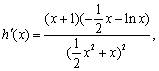 令
令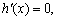 得
得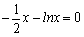 .
.
设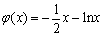 ,因为
,因为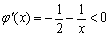 ,所以
,所以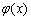 在
在 上单调递减,
上单调递减,
不妨设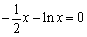 的根为
的根为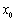 .当
.当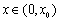 时,
时,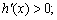 当
当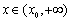 时,
时,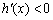 .
.
所以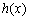 在
在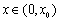 上是增函数;在
上是增函数;在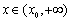 上是减函数.
上是减函数.
所以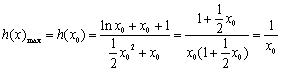 .
.
因为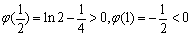

所以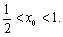 此时
此时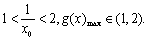 所以
所以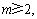 即整数
即整数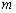 的最小值为2
的最小值为2
(Ⅲ)当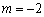 时,
时,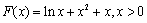
由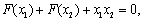 即
即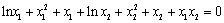
从而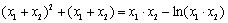
令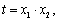 则由
则由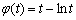 得,
得,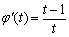
可知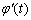 在区间(0,1)上单调递减,在区间
在区间(0,1)上单调递减,在区间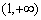 上单调递增。所以
上单调递增。所以
所以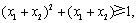 即
即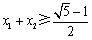 成立.
成立.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
某餐厅的原料费支出 与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为
与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为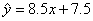 ,则表中的m的值为
,则表中的m的值为
|
| 2 | 4 | 5 | 6 | 8 |
|
| 25 | 35 |
| 55 | 75 |
A.50 B.55 C.60 D.65
 中,
中, 分别为内角
分别为内角 所对的边,若
所对的边,若

 ,则角
,则角 的取值范围是
的取值范围是  ,则
,则 = 0 ;不等式
= 0 ;不等式 的解集为______.
的解集为______. 的右支上任意一点,由P向两条渐近线作平行线交渐近线于M、N两点,若平行四边形OMPN面积为3,则双曲线的离心率为 .
的右支上任意一点,由P向两条渐近线作平行线交渐近线于M、N两点,若平行四边形OMPN面积为3,则双曲线的离心率为 . 为等差数列,且
为等差数列,且 ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 、
、 两个小孩和甲、乙、丙三个大人排队,
两个小孩和甲、乙、丙三个大人排队,

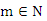 , 如题“m>0,则方程
, 如题“m>0,则方程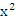
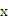
 有实根的逆否命题是
有实根的逆否命题是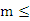
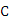 若方程
若方程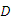 若方程
若方程