Question

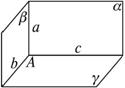
三个平面两两相交得三条直线，求证：这三条直线相交于同一点或两两平行.

已知：平面α∩平面β＝a，平面β∩平面γ＝b，平面γ∩平面α＝c.

求证：a、b、c相交于同一点，或a∥b∥c.

 

Answer 1

答案：
解析：

证明：∵α∩β＝a，β∩γ＝b ∴a、bβ ∴a、b相交或a∥b. (1)a、b相交时，不妨设a∩b＝P，即P∈a，P∈b 而a、bβ，aα ∴P∈β，P∈α，故P为α和β的公共点 又∵α∩γ＝c 由公理2知P∈c ∴a、b、c都经过点P，即a、b、c三线共点. (2)当a∥b时 ∵α∩γ＝c且aα，aγ ∴a∥c且a∥b ∴a∥b∥c 故a、b、c两两平行. 由此可知a、b、c相交于一点或两两平行.