题目内容
椭圆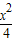
+
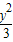=1上有n个不同的点P1，P2，P3，…，Pn，F是右焦点，|P1F|，|P2F|，…，|PnF|组成等差数列，且公差d＞
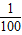，则n的最大值是（ ）A．99
B．100
C．199
D．200
【答案】分析：利用等差数列的通项公式和|PiF|的最大值和最小值分别为a+c，a-c，即可得出．
解答：解：∵|P1F|，|P2F|，…，|PnF|组成等差数列，∴|PnF|=|P1F|+（n-1）d．
∵|PnF|≤a+c，|P1F|≥a-c，
∴|PnF|-|P1F|≤（a+c）-（a-c）=2c=2，
又公差d＞
，
∴
，
∴n的最大值是200．
故选D．
点评：熟练掌握椭圆的性质、等差数列的通项公式是解题的关键．
解答：解：∵|P1F|，|P2F|，…，|PnF|组成等差数列，∴|PnF|=|P1F|+（n-1）d．
∵|PnF|≤a+c，|P1F|≥a-c，
∴|PnF|-|P1F|≤（a+c）-（a-c）=2c=2，
又公差d＞
，∴
，∴n的最大值是200．
故选D．
点评：熟练掌握椭圆的性质、等差数列的通项公式是解题的关键．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
椭圆
+
=1上有n个不同的点：P1，P2，…，Pn，椭圆的右焦点为F，数列|PnF|是公差不小于
的等差数列，则n的最大值是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 100 |
| A、198 | B、199 |
| C、200 | D、201 |
+
=1上有n个不同的P1,P2,P3,……Pn,设椭圆的右焦点为F，数列{|FPn|}的公差不小于
的等差数列，则n的最大值为 ．